Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.5 - Ex. 56

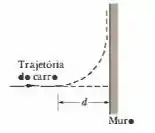
Frear ou desviar? A Fig. 6-44 mostra uma vista superior de um carro que se aproxima de um muro. Suponha que o motorista começa a frear quando a distância entre o carro e o muro é d =   107   m , que a massa do carro é m   =   1400   k g , que a velocidade inicial é v 0   =   35   m / s e que o coeficiente de atrito estático é μ s   = 0,50 . Suponha também que o peso do carro está distribuído igualmente pelas quatro rodas, mesmo durante a frenagem. (a) Qual é o valor mínimo do módulo do atrito estático ( entre os pneus e o piso) para que o carro pare antes de se chocar com o muro? (b) Qual é o valor máximo possível do atrito estático ? (c) Se o coeficiente de atrito cinético entre os pneus (com as rodas bloqueadas) e o piso é μ k   =   0,40 , com que velocidade o carro se choca com o muro? O motorista também pode tentar se desviar do muro, como mostra a figura. (d) Qual é o módulo da força de atrito necessária para fazer o carro descrever uma trajetória circular de raio d e velocidade v 0 ?(e) A força calculada no item (d) é menor que f s , m á x , o que evitaria o choque?

Passo 1

Então galera , como o movimento é uniformemente variado sabemos que a velocidade do carro é dada por v 2 = v 0 2 + 2 a d . Fazendo v   =   0 , v 0 =   35   m / s e d   =   107   m , obtemos a = - 5,72   m / s 2 como a aceleração mínima necessária para que o carro pare a tempo. Assim, a força de atrito mínima necessária para que o carro pare a tempo é :

f = m a = 1400 k g 5,72 m s 2 ≅ 8,0 * 10 3 N

De boa até aqui , pessoal? Bora continuar que ainda não acabou!

Passo 2

Nós sabemos que o valor máximo possível do atrito estático é dado por :

f s , m á x = μ s m g = 0,50 1400 k g 9,8 m s 2 ≅ 6,9 * 10 3 N

Passo 3

Bom pessoal , se μ k = 0,40 , f k =   μ k m g e a aceleração é a =   - μ k g . Podemos achar a velocidade com a qual o carro se choca com o muro através da relação :

v = v 0 2 + 2 a d = 35 m s 2 - 2 * 0,4 * 9,8 m / s 2 * 107 ≅ 20   m s o u 72   k m h

Passo 4

Podemos achar a força necessária para que o carro descreva a trajetória circular que evitaria o choque através da relação :

F r = m v o 2 r = 1400 k g 35 m s 2 107   m = 1,6 * 10 4 N

Passo 5

Então pessoal , como F r > f s , m á x , a manobra não é possível

Tranquilo galera?? Bora resolver mais questões então!!!!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No Exemplo 5.8, investigamos as forças que uma criança experimenta em uma roda-gigante. Suponha que os dados daquele exemplo se apliquem a este problema. Que força (módulo e direção) o assento exerce
Uma estudante constrói e calibra um acelerômetro e o usa para determinar a velocidade do seu carro em uma determinada curva da estrada sem inclinação. Acelerômetro é um fio com uma esfera de chumbo e
Em uma secadora de roupas doméstica, um tubo cilíndrico contendo roupas molhadas é girado regularmente sobre um eixo horizontal, como mostrado na Figura P5.41. Para que as roupas sequem uniformemente,
Como a Terra gira sobre seu eixo, um ponto no equador experimenta uma aceleração centrípeta de 0,0337m / s 2 , enquanto um ponto nos polos não experimenta nenhuma aceleração centrípeta. Se uma pessoa
Um disco de massa m 1 é amarrado a um barbante e girado em um círculo de raio R em uma mesa horizontal e sem atrito. A outra ponta do barbante passa por um pequeno furo no centro da mesa e um corpo de