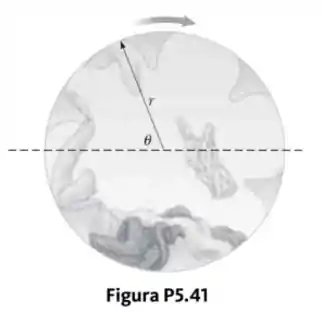
Em uma secadora de roupas doméstica, um tubo cilíndrico contendo roupas molhadas é girado regularmente sobre um eixo horizontal, como mostrado na Figura P5.41. Para que as roupas sequem uniformemente, elas tombam. A taxa de rotação do tubo de paredes planas é escolhida de modo que uma pequena peça de roupa perderá contato com o tubo quando estiver a um ângulo de acima da horizontal. Se o raio do tubo é , que taxa de revolução é necessária?

E aiii gente, tudo bom com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo e bora!

Quando a roupa está em um ângulo mais baixo, a componente radial de é:

Em , a força normal cai a zero e :