Frequentemente, o núcleo filho de um núcleo pai de um átomo radioativo é também radioativo. Suponha que o núcleo pai, chamado de , tem uma constante de decaimento , enquanto o núcleo filho, chamado de , tem uma constante de decaimento O número de núcleos filho são dados pela solução de uma equação diferencial:

Onde é número de núcleos pai.

1. Justifique esta equação diferencial.
2. Mostre que a solução para esta equação é:

Onde é o número de núcleos pai presentes em quando não existem núcleos filhos.

3. Mostre que a expressão para na parte (b) dá se ou .
4. Faça um gráfico de e como função do tempo quando onde são as vidas médias dos núcleos pai e filho, respectivamente.

Letra (b):

Para verificar se uma expressão é solução de uma equação diferencial precisamos substituir a função (e sua derivada) na equação e encontrar uma igualdade.

Então vou começar diferenciando a potencial solução com respeito ao tempo:

E agora vou substituir essa derivada na equação diferencial do passo , e precisamos lembrar que . Do passo um:

Substituindo a derivada no lado esquerdo, a função no lado direito da equação e temos:

Vou multiplicar os dois lados por e simplificar o que der, saca só:

E vou simplificar mais um pouco o lado direito:

E agora vou colocar em evidência no lado direito e assim obter uma igualdade:

Como encontramos uma igualdade, significa que a solução dada no problema é realmente uma solução da equação diferencial.

Letra (c):

A expressão que queremos analisar é:

Temos a multiplicação de dois fatores, então teremos positivo se ambos forem ou positivos ou negativos, certo?

Se o denominador e a expressão dentro dos parênteses serão negativos para qualquer . Se tanto o denominador quanto a expressão dentro dos parênteses serão positivas para .

Letra (d):

As funções a serem esboçadas em um gráfico são:

Com a ajuda de um programa um gráfico com as duas funções é mais ou menos assim:

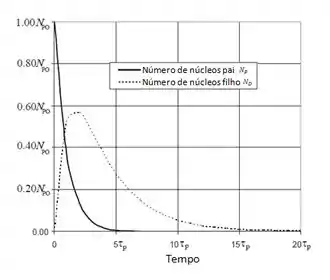
Espero ter ajudado!

Até a próxima =)