Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.5 - Ex. 14
A função posição de uma partícula que está se movendo ao longo do eixo é , com em metros e em segundos. (a) Em que instante e (b) em que posição a partícula para (momentaneamente)? Em que (c) instante negativo e (d) instante positivo a partícula passa pela origem? (e) Plote o gráfico de em função de para o intervalo de a . (f) Para deslocar a curva para a direita no gráfico, devemos acrescentar a o termo ou o termo ? (g) Essa modificação aumenta ou diminui o valor de para o qual a partícula para momentaneamente?
Passo 1
Galera, para saber em qual instante uma partícula para é só igualar sua velocidade a zero. Para encontrar a função velocidade é só derivar a função posição em relação ao tempo.
Agora é só igualar a zero.
Para saber a posição da partícula nesse instante, devemos substituir o valor de encontrado na função posição.
Passo 2
A partícula passar pela origem é sua posição ser igual a zero.
Passo 3
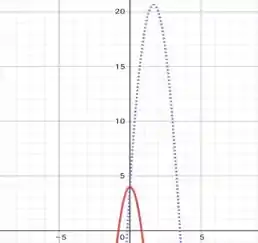
O gráfico mostra a função em vermelho e o gráfico em azul . Podemos observar que:
(f) Adicionando o gráfico foi deslocado para direira;
(g) O ponto crítico do gráfico, o seja, o topo onde a partícula para o que aumenta o valor de em que.
Agora devemos substituir em para encontra a posição que a partícula para na nova equação.
Resposta
a)
b)
c)
d)
e)
f)
g) Aumenta para