Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 8.Problemas - Ex. 7
Um gafanhoto, pousado na beirada superior de uma folha que está boianda sobre a água de um tanque, salta, com velocidade inicial de , em direção à beirada inferior da folha, no sentido do comprimento. As massas do gafanhoto e da folha são de e , respectivamente, e comprimento da folha é de . Em que domínio de valores pode estar compreendido o ângulo entre a direção do salto e a sua projeção sobre a horizontal para que o gafanhoto volte a cair sobre a folha?
Passo 1
O primeiro passo em problemas assim é fazer um desenho para entender a situação! Acompanhe a figura a seguir:
Coloquei a origem do sistema de coordenadas na posição em que estava a extremidade da folha e o gafanhoto imediatamente antes do pulo. O gafanhoto vai pular com uma velocidade que forma um ângulo com a horizontal. Portanto,
Com isso, o momento linear do gafanhoto imediatamente após o pulo é
Mas o conjunto folha + gafanhoto estava inicialmente em repouso. Isso significa que o momento linear do sistema era nulo antes do pulo. Portanto, aplicando a conservação do momento, podemos escrever
Olhando apenas para a direção :
Essa é a velocidade de recuo da folha:
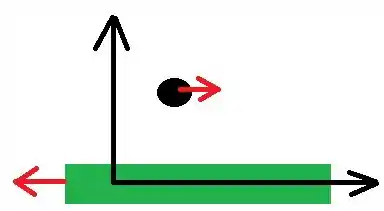
Enquanto o gafanhoto se move no ar, a folha se move para trás. Note que a origem do sistema de coordenadas permanece no mesmo lugar.
Passo 2
Vamos calcular agora o tempo que o gafanhoto permanece no ar. Sabemos que ele salta com uma velocidade que será constante na horizontal (MRU) e uma velocidade inicial que não será constante na vertical (MRUV).
Sabemos que no movimento vertical, podemos usar as equações do MRUV. Na subida, temos que:
Quando o gafanhoto atinge a altura máxima, temos que . Assim, o tempo de subida é
O tempo total que o gafanhoto permanece no ar é
Nesse intervalo de tempo, a distância horizontal percorrida por ele é
Usando que , temos que
Passo 3
Mas ao mesmo tempo que o gafanhoto se move para frente e percorre uma distância , a folha anda para trás e percorre uma distância :
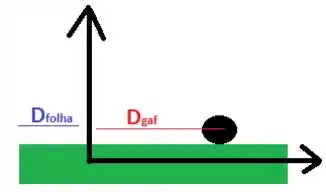
Como o tempo para que isso aconteça é e a velocidade da folha em módulo é constante e igual a
A distância percorrida pela folha é
Olhando a figura, vemos que a condição para que o gafanhoto caia sobre a folha é que
onde é o comprimento da folha. Se a soma dessas distâncias for maior que o comprimento da folha, o gafanhoto cairá fora dela! Agora é só usar as expressões que encontramos:
Assim,
Logo,
Passo 4
Agora podemos substituir os números: , , , e :
Temos que descobrir qual ângulo tem seno . O ângulo correspondente é . Agora olhe o desenho a seguir:
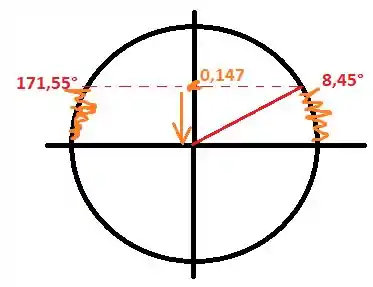
Olhando para o círculo trigonométrico, vemos que os intervalos que satisfazem a inequação são:
Assim,
Se o ângulo não estiver nesses intervalos, o gafanhoto cai fora da folha!