Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 5.Problemas - Ex. 10

No sistema da figura, m 1 = 1   K g ,   m 2 = 3 K g   e   m 3 = 2   K g , e as massas das polias e das cordas são desprezíveis. Calcule as acelerações a 1 ,   a 2   e   a 3 das massas m 1 ,   m 2   e   m 3 , e a tensão T da corda.

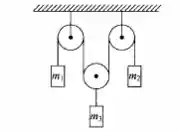
Passo 1

Bora treinar um pouquinho de dinâmica, hehe. Aqui a ideia é perceber que a quantidade de cabo é a mesma a todo momento no nosso sistema, ok? Então

x 1 + x 2 + 2 x 3 = k

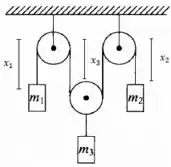
Derivando tudo em relação ao tempo podemos relacionar as acelerações de cada um

d 2 x 1 d t 2 + d 2 x 2 d t 2 x 2 + 2 d 2 x 3 d t 2 = d 2 k d t 2

a 1 + a 2 + 2 a 3 = 0  

Além disso, vamos visualizar o diagrama de forças para escrever nossas equações, chega mais!

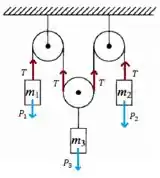
Vamos supor um sentido de aceleração para os corpos, todos para cima. Caso tenhamos suposto errado seu resultado será negativo e indica um movimento na direção oposta, simplesmente. Vem comigo!

  • Corpo 1 :   T - g = m 1 a 1 = a 1
  • Corpo 2 : T - 3 g   = m 2 a 2 = 3 a 2
  • Corpo 3 : 2 T - 2 g = m 3 a 3 = 2 a 3

Temos um sistema com 4 incógnitas e e 4 equações se contarmos com nossa primeira dedução lá em cima, vamos só organizar e por a mão na massa.

T - g = a 1 T - 3 g   = 3 a 2 2 T - 2 g = 2 a 3 a 1 =   - 2 a 3 + a 2

Que pode ser rescrito como

T - g = a 1 T - 3 g 3   = a 2 T - g = a 3 a 1 =   - 2 a 3 + a 2

Passo 2

Substituindo as acelerações das 3 primeiras equações na quarta vamos ter o seguinte

T - g = - 2 T - g + T - 3 g 3

T - g = - 2 T + 2 g - T 3 + g

T + 2 T + T 3 = 3 g + g

10 T 3 = 4 g → T = 12 10 g = 1,2 g

E aí podemos substituir em cada uma das acelerações

a 1 = T - g = 1,2 g - g = 0,2 g

a 2 = T - 3 g 3 = 1,2 g - 3 g 3 = - 0 , 6 g

a 3 = T - g = 1,2 g - g = 0,2 g

Resposta

a 1 = 0,2 g

a 2 = - 0 , 6 g

a 3 = 0,2 g

T = 1,2 g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura 5.60, um trabalhador levanta um peso p puxando uma corda para baixo com uma força F → . A polia superior está presa ao teto por meio de uma corrente, e a polia inferior está presa ao peso po
Na Figura P5.114, as massas m 1 e m 2 está conectadas por um fio leve A que passa sobre uma polia leve e sem atrito B. O eixo da polia B é conectado por um segundo fio leve C que passa sobre uma segun
Determine a força P necessária para suportar  a massa  de  20  kg  usando  a  talha  do  tipo   “Spanish Burton”. Além disso, quais  são  as  reações nos  ganchos de apoio A, B e C?
Determine a  força P necessária para manter a  massa de 50 kg em equilíbrio.
Os princípios de uma talha diferencial são indicados esquematicamente na fi gura. Determine a intensidade da  força P necessária para suportar  força  de 800 N. Além disso, encontre a distância x onde