Uma garota de desliza pelo escorregador de um parquinho com uma queda vertical de . Quando ela atinge a base do escorregador, a rapidez dela é . (a) Quanta energia foi dissipada por atrito? (b) Se o escorregador está inclinado a com a horizontal, qual é o coeficiente de atrito cinético entre a garota e o escorregador?

De forma geral, a energia mecânica de um objeto é a soma da energia potencial gravitacional, a elástica e a energia cinética:

Não há molas no nosso problema, então a gente descarta . Sobra apenas a energia cinética e a energia potencial gravitacional para avaliarmos os dois momentos do nosso problema.

Inicialmente, a menina está em repouso, então a energia cinética inicial dela é nula. Sobra então a energia potencial gravitacional, dada por . Então temos:

Subsituindo nossos dados:

No segundo momento, na base do escorrega, a menina está na altura . Ou seja, a energia potencial gravitacional é nula. Então fica apenas a energia cinética dada por

Substituindo os dados:

A variação de energia fica:

Então a energia dissipada é:

(b) Para gerar essa variação de energia da menina, é preciso que alguma força realize trabalho sobre ela. Nesse caso, essa tarefa será cumprida pela força de atrito cinético, que tem essa fórmulinha:

Para achar a expressão da força normal sobre a menina, podemos fazer um diagrama de corpo livre:

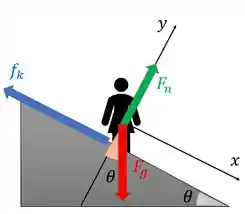
Para achar , a gente aplica a segunda lei de Newton no eixo , onde ela está. Não há movimento nessa direção, então . Aí temos

Sendo :

Substituindo isso na força de atrito:

O que queremos é esse coeficiente de atrito .

Agora para achar esse coeficiente, já que temos a variação de energia, podemos usar o teorema trabalho-energia para o nosso caso:

Sendo que a variação de energia é a que achamos no item (a):

E o trabalho externo é o trabalho feito pela força de atrito. Como ela é uma força constante e aplicada na mesma direção onde movimento de extensão acontece, podemos usar:

Substituindo a expressão de :

Esse trabalho é negativo porque ele é contrário ao movimento (faz a menina acelerar menos).

Só que quem é esse ? Olha de novo a figura:

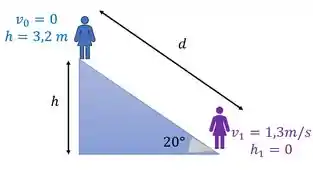
A gente pode usar trigonometria para dizer:

Substituindo na expressão do trabalho:

Como :

Substituindo tudo o que a gente tem no teorema:

Substituindo os dados e isolando :