Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 73

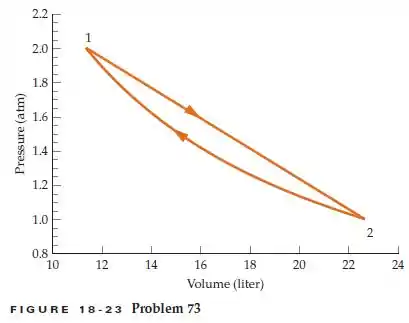
Uma amostra de 1 mol de gás diatômico se expande. Esta expansão é representada pela linha reta de 1 até 2 no diagrama PV (Figura 18-23). Depois, o gás é comprimido isotermicamente. Esta compressão é representada pela linha curva de 2 até 1 no diagrama PV. Calcule o trabalho realizado pelo gás a cada ciclo.

Passo 1

Bom, o exercício nos pede o trabalho total do semi-círculo. O trabalho total pode ser calculado como a área dessa figura geométrica, que nós não sabemos.

Então vamos com calma, para calcular o trabalho total podemos calcular toda a área abaixo do caminho 1 → 2 , e subtraírmos do trabalho feito pelo caminho de 2 → 1 .

W t o t a l = W 1 → 2 - W 2 → 1

Começamos pelo trabalho W 1 → 2 , que forma um trapézio:

W 1 → 2 = A t r a p é z i o = 1 2 B m a i o r + B m e n o r . A l t u r a

W 1 → 2 = 1 2 2   a t m + 1   a t m . 23   L - 11,5 L = 17,3   a t m . L   x 101,325   J a t m   .   L

W 1 → 2 = 1,75   k J

Para a compressão adiabática temos uma fórmula pré-estabelecida:

W 2 → 1 = n R T ln ⁡ V 1 V 2

Não temos T, mas temos tudo o que precisamos para calculá-la pela lei dos gases:

P 1 V 1 = n R T 1

Substituindo:

2   a t m   x   101325   P a 1   a t m ( 11,5   x   10 - 3 m ³ ) = ( 1   m o l ) 8,314 J m o l . K T

T = 280   K

No trabalho:

W 2 → 1 = 1   m o l 8,314 J m o l . K 280   K ln ⁡ 11,5   L 23   L = - 1 , 61   k J

Como estamos trabalhando com a área:

W 2 → 1 = 1,61   k J

No trabalho total:

W t o t a l = 1,75   k J - 1,61   k J = 0,14   k J

Assumimos aqui que quando o círculo está girando no sentido horário o trabalho total é positivo. No entanto se assumíssemos que girar no sentido contrário gera trabalho negativo, nosso resultado seria:

W t o t a l = - 0,14   k J

Resposta

W t o t a l = 0,14   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra um ciclo fechado de um gás (a figura não foi desenhada em escala). A variação da energia interna do gás ao passar de a para c ao longo da trajetória a b c é - 200 J . Quando o gás pass
Um sistema termodinâmico passa do estado A para o estado B do estado B para o estado C e de volta para o estado A , como mostra o diagrama p - V da Figura abaixo. A escala do eixo vertical é definida
Um gás ideal, a uma temperatura inicial T 1 e com um volume inicial de 2,0m 3 , sofre uma expansão adiabática para um volume de 4,0m 3 , depois uma expansão isotérmica para um volume de 10m 3 e, final
Um gás ideal é submetido a um ciclo completo em três etapas: expansão adiabática com um trabalho de 125J , contração isotérmica a 325K e aumento de pressão a volume constante. (a) Plote as três etapas
Uma amostra com 3,00m o l s de um gás ideal está inicialmente no estado 1 à pressão p 1 = 20,0a t m e volume V 1 = 1500c m 3 . Primeiro, o gás é levado ao estado 2 com pressão p 2 = 1,50 p 1 e volume