Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 21.Exercícios e Problemas - Ex. 18
Generalização da fórmula . Considere um circuito fechado de forma genérica contido em um plano, transportando uma corrente . Este circuito pode ser substituído aproximadamente por um conjunto de circuitos retangulares, todos transportando a mesma corrente , como mostra a Figura 21.13.
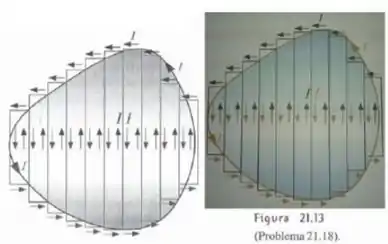
a) Mostre que o dipolo magnético do conjunto de circuitos retangulares é o produto da corrente pela área do polígono que contorna todos eles.
b) Mostre que quando os circuitos retangulares se tornam infinitamente estreitos a área do polígono é igual a área do circuito curvo.
Passo 1
Fala galera, tudo bem?
Esse é um exercício um pouco mais teórico, então se você quiser pular ele tudo bem...
Para fazer o item (a) vou considerar apenas 2 retângulos pois acho que assim fica um pouco mais simples e a generalização é imediata.
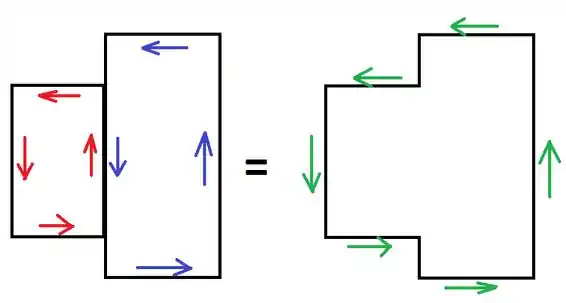
Eu acho que o desenho em si explica melhor do que qualquer coisa que eu possa explicar, mas a ideia é a seguinte: a gente pode pensar no circuito completo (corrente em verde) como sendo dividido em dois retângulos, um com a corrente em vermelho e outro com a corrente em azul. Na lateral que junta os dois retângulos as correntes se anulam, de modo que as duas situações são equivalentes!
Do lado esquerdo, o dipolo magnético de cada espira é
Somando os dois, temos
Mas sabemos que , de modo que
Com isso, achamos o dipolo magnético total do circuito e mostramos o que o item (a) pede no caso de dois retângulos. É só você repetir o raciocínio e ir adicionando retângulos e pronto, você prova para um número qualquer de retângulos!
Passo 2
O item (b) é mais de matemática do que física, né? A ideia por trás dele é a mesma da soma de Riemann quando a gente brinca com integral lá em cálculo 1...
Vou pegar o seguinte problema: queremos saber a área sob o gráfico de uma curva dada por . A ideia básica é subdividir ao intervalo em vários pequenos intervalos com
onde é o número de subintervalos. Daí, pegamos um ponto dentro de um dos intervalos e construímos um retângulo de base e altura , cuja área será
Daí, aproximamos a área sob a curva como sendo a soma das áreas desses retângulos:
Conforme a gente vai aumentando , melhor nossa aproximação fica:
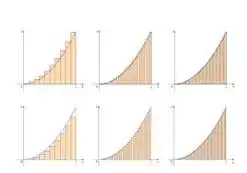
No limite de “infinitos” retângulos, a soma se torna uma integral e dá exatamente a área sob a curva:
Isso é exatamente o que ele pede para fazer no item (b). Problema resolvido!
Resposta
Demonstração.