Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 18.Exercícios e Problemas - Ex. 17

Calcule:

a) a polarização elétrica em cada um dos dielétricos do capacitor visto na Figura 18.23;

b) a densidade superficial de carga de polarização na interface entre os dois dielétricos.

Passo 1

Eai pessoal, beleza?

No exercício 16 nós calculamos o vetor deslocamento elétrico entre as placas do capacitor:

D → = - Q A   y ^

Por uma questão de comodidade, vamos definir um sistema de coordenadas:

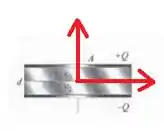
Para 0 < y < d / 2 temos o dielétrico 1 com constante dielétrica κ 1 e para - d / 2 < y < 0 temos o dielétrico 2.

Para relacionar a polarização P → com o deslocamento elétrico D → , recorremos a expressão:

D → = ϵ 0 E → + P →               e             P → = ϵ 0 κ - 1   E →

Assim,

ϵ 0 E → = P → κ - 1

Logo,

D → = P →   1 κ - 1 + 1 → D → = κ κ - 1 P →

Ou ainda,

P → = κ - 1 κ D →

Com isso, para cada dielétrico teremos uma polarização diferente:

P → = - κ 1 - 1 κ 1 Q A   y ^ ,               0 < y < d 2 - κ 2 - 1 κ 2 Q A   y ^ ,             - d 2 < y < 0

Esse foi o item (a), agora partiu item (b)!!!

Passo 2

Para encontrar a densidade superficial de cargas de polarização entre os dois meios nós usamos a equação 18.30 apresentada no livro:

D κ 2 - D κ 1 = ϵ 0 σ P

Com isso,

σ P = D ϵ 0 1 κ 2 - 1 κ 1 = D ϵ 0 ⋅ κ 1 - κ 2 κ 1 κ 2

Daí, usando D = Q / A , encontramos

σ P = κ 1 - κ 2 Q κ 1 κ 2 ϵ 0 A

E assim fechamos mais um problema 😉.

Resposta

P → = - κ 1 - 1 κ 1 Q A   y ^ ,               0 < y < d 2 - κ 2 - 1 κ 2 Q A   y ^ ,             - d 2 < y < 0

σ P = κ 1 - κ 2 Q κ 1 κ 2 ϵ 0 A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 25-49 mostra um capacitor de placas paralelas com uma área das placas A = 10,5 c m 2 e uma distância entre as placas 2 d = 7,12 m m . O lado esquerdo do espaço entre as placas é preenchido por
Um capacitor de placas paralelas cujo dielétrico é o ar tem urna capacitância de 50 p F . (a) Se a área das placas é 0,35 m 2 , qual é a distância entre as placas? (b) Se a região entre as placas é pr
Na Fig. 25 -46, qual é a carga armazenada nos capacitares de placas paralelas se a diferença de potencial da bateria é 12,0 V ? O dielétrico de um dos capacitores é o ar; o do outro, uma substância co
O leitor dispõe de duas placas de cobre, uma folha de mica (espessura = 0,10 mm, K = 5,4), um pedaço de vidro (espessura = 2,0 mm, K = 7,0) e um bloco de parafina (espessura = 1,0 cm, K = 2,0) . Para
Um capacitor de placas paralelas de área A e espaçamento D tem, inserida entre elas, uma lâmina de dielétrico de mesma área A , de constante elétrica κ e espessura dD . Demonstre que a capacitância do