Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 9.Problemas - Ex. 1
O tubo de vidro de um barômetro de mercúrio tem secção reta de e de altura acima da superfície livre do reservatório de mercúrio. Num dia em que a temperatura ambiente é de e a pressão atmosférica verdadeira é de, a altura da coluna barométrica é de . Calcule a quantidade de ar (em moles) aprisionada no espaço acima da coluna de mercúrio.
Passo 1
Vamos começar com um desenho da situação:
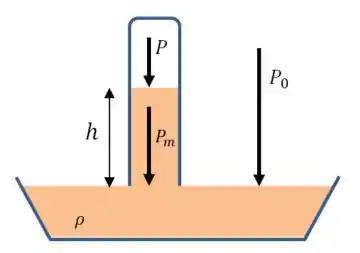
Para que o sistema esteja em equilíbrio, as pressões devem se igualar da seguinte forma:
A pressão atmosférica corresponde à pressão de uma coluna de mercúrio com altura , então:
Já a coluna do tubo no desenho tem , então:
Passo 2
Com essas duas equações, podemos definir uma relação entre e :
Substituindo isso na primeira equação, temos o seguinte:
E como a pressão atmosférica em Pascal é , temos:
Passo 3
Mas nosso objetivo é calcular o número de moles na parte de cima do tubo. Vamos usar a lei dos gases ideais:
Já temos a temperatura e a pressão. Podemos calcular o volume com os valores que foram dados no enunciado:
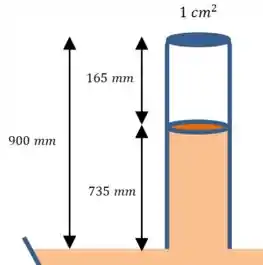
A temperatura em Kelvin é , então podemos substituir os valores numéricos:
Onde usamos .
Resposta
No espaço acima da coluna de mercúrio há de ar.