Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 18
Um giroscópio, constituído por um disco de de raio, colocado no centro de uma haste de de comprimento e massa desprezível . Ele é colocado com seu eixo horizontal e um externo apoiado num suporte (Fig. da pg.271) Calcule a velocidade angular de precessão, em.
Passo 1
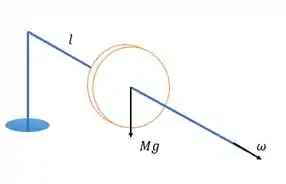
Para calcular a força de precessão, temos:
Nesse caso, temos:
E para o momento de inércia do disco:
Para o :
Passo 2
Arrumando as coisas:
Substituindo os valores, temos:
Isto é,
Resposta
Exercícios de Livros Relacionados
Um certo giroscópio é formado por um disco homogêneo com 50c m de raio montado no centro de um eixo de 11c m de comprimento e massa desprezível. O eixo está na posição horizontal, apoiado em uma das e
Um pião gira a 30r e v / s em torno de um eixo que faz um ângulo de 30 ° com a vertical. A massa do pião é 0,50k g , o momento de inércia em relação ao eixo central é 5,0 × 10 - 4k g ∙ m 2 e o centro
Um giroscópio possui movimento de precessão em torno de um eixo vertical. Descreva o que ocorre com a velocidade angular de precessão quando são feitas as seguintes mudanças nas variáveis, mantendo-se
Um giroscópio na Lua. Certo giroscópio realiza precessão a uma taxa de 0,50r a d / s quando usado na Terra. Se fosse levado para uma base lunar, onde a aceleração da gravidade é 0,165g , qual seria a
Um giroscópio de demonstração pode ser construído retirando-se o pneu de uma roda de bicicleta com diâmetro de 0,650 m, enrolando-se um fio de chumbo no aro e fixando-o nele. O eixo se projeta 0,200 m