Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 48

Um recipiente com o fundo espelhado está cheio com um líquido de índice de refração igual a 1,63 . Um feixe de luz atinge a superfície superior do líquido formando um ângulo de 42,5 ° com a normal. O feixe atravessa a camada de líquido, reflete-se na superficie espelhada no fundo do recipiente e retorna para a superficie; qual é o ângulo que o feixe emergente forma com a normal da superfície superior do líquido?

Passo 1

Opa!!

Aqui temos uma serie de refração e reflexão. Então vamos fazer um desenho para ajudar:

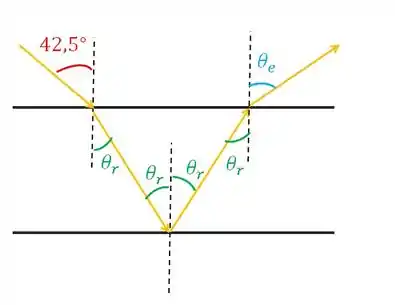
Os θ r iguais ali no meio vêm de propriedades de retas paralelas cortadas por transversais. Além da propriedade de que o ângulo de incidência é igual ao ângulo de reflexão.

Queremos saber o ângulo emergente θ e .

Passo 2

Aplicando a lei de snell na interface ar-liquido:

n a r sen ⁡ 42,5 ° = n l i q sen ⁡ θ r

1 ⋅ sen ⁡ 42,5 ° = 1,63 ⋅ sen ⁡ θ r

sen ⁡ θ r = 0,41

Show! Vamos deixar assim com o seno mesmo.

Agora, vamos aplicar a lei de snell na interface liquido-ar:

n l i q sen ⁡ θ r = n a r sen ⁡ θ e

1,63 ⋅ 0,41 = 1 ⋅ sen ⁡ θ e

Resolvendo isso:

θ e = 42,5 °

Prontinhos!! Sucesso?!

Resposta

θ e = 42,5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um raio de luz proveniente do ar incide sobre um bloco de um material sólido transparente cujo indice de refração é n . Sabendo que n = 1,38 , qual deve ser o maior ângulo de incidência θ a para que o
A luz que atravessa um material de indice de refração n 1 incide com um ângulo θ 1 , em relação à normal sobre a interface com um bloco de material que possui lados paralelos e índice de refração n 2
Uma placa de vidro com espessura de 2.50m m e um índice de refração de 1,40 é colocada entre uma tela e uma fonte de luz puntiforme de comprimento de onda igual a 540n m (no vácuo). A distância entre
Você olha para dentro de um recipiente de vidro com paredes verticais de modo que o seu olhar vá da borda superior até a extremidade oposta no fundo (Figura 33.48a). O recipiente é um cilindro oco com
Um feixe de luz incide normalmente sobre uma das faces menores de um prisma com ângulos de 30 ° ,60 °e90 ° (figura 33.50). Uma gota de um líquido é colocada sobre a hipotenusa do prisma. Sabendo que o