Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 10.Problemas - Ex. 5

O diâmetro angular aparente do Sol visto da Terra (ângulo subentendido pelo disco solar) é de 0,55 ° . Utilizando apenas estes dados, juntamente com o período da órbita da Terra em torno do Sol, aproximada por um circulo, calcule a densidade média μ do Sol.

Passo 1

Como que fica o Sol visto da Terra? Fica uma parada meio assim, né?

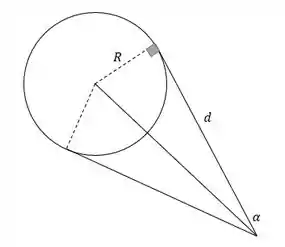
Bom, mas a Terra e o Sol são beeeeem distantes, né? Então a gente vai considerar que esses raios que chegam são quase paralelos, pra gente fazer aparecer esse tal “diâmetro angular”.

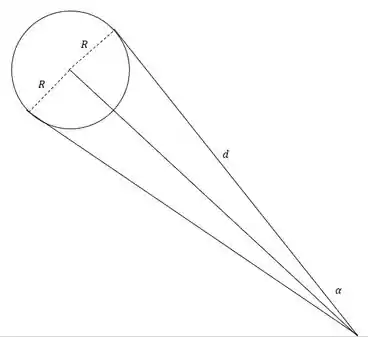
Sacou o que é? Como os raios vão ser quase paralelos, por causa da distância, vão encontrar o Sol quase que diametralmente opostos, e aí vai aparecer esse diâmetro.

Passo 2

Agora vamos pras contas! Aquele ângulo α fica dividido em duas partes iguais, de forma que:

t g α 2 = R d

Mas esse ângulo é extremamente pequeno, né? Pensa bem, 0.55 ° . É muito pequeno! Pra esses ângulos pequenos, a gente pode usar que

t g n x = n t g x

Daí, pra gente achar a tangente de α , é só multiplicar aquela parada por 2 .

t g 2 α 2 = 2 t g α 2

t g α = 2 R d

d = 2 R t g ( α )

Passo 3

Olha aí pra gravitação agora. A Terra orbita em torno do Sol, de forma que a centrípeta é igual ao peso.

m ω 2 d = G M m d 2

ω 2 d 3 = G M

2 π T 2 2 R t g α 3 = G 4 3 ρ π R 3

4 π 2 T 2 8 R 3 t g 3 α = 4 G ρ π R 3 3

Agora vamos cortar tudo que tem pra cortar e botar em função do ρ , que é o que a gente quer!

ρ = 24 π G T 2 t g 3 α

O período é T = 365   d i a s , que precisa ser passado pra segundos. Substituindo e fazendo as contas:

ρ = 1.3 × 10 3 k g m 3

Resposta

ρ = 1.3 × 10 3 k g m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

À medida que Marte percorre sua órbita elíptica em torno do Sol, sua distancia mais próxima do centro do Sol (no periélio) é igual a 2,067 × 10 11m , e sua distancia máxima ao centro so Dol (no afélio
Duas estrelas idênticas, cada uma com massa M 1 e a outra com massa M 2 , descrevem uma órbita circular em torno do centro de massa delas. A estrela de massa M 1 possui órbita com raio R 1 , e a estre
Duas estrelas idênticas, cada uma com massa M, giram em torno do centro de massa das duas estrelas. Cada órbita é circular e possui raio R, de modo que as duas estrelas estão sempre em lados opostos d
Um módulo de aterrissagem lunar, de 4.000k g , encontra-se em órbita 50k m acima da superfície da Lua. Ele deve passar para uma órbita de 300k m de altitude a fim de se conectar à nave-mãe, que levará
A NASA gostaria de colocar um satélite em órbita em torno da Lua de forma que ele permanecesse numa mesma posição acima da superfície lunar. Qual é a altitude da órbita do satélite?