Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.1 - Ex. 11
Um homem empurra um piano de , de modo que ele desliza com velocidade constante para baixo de uma rampa inclinada de acima da horizontal. Despreze o atrito que atua sobre o piano. Calcule o módulo da força aplicada pelo homem, se ela for:
a) paralela ao plano inclinado e
b) paralela ao piso.
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
O enunciado nos disse que um homem está empurrando um piano de de massa e que esse piano desliza com velocidade constante para baixo de uma rampa que faz com a horizontal. E aí ele quer que a gente calcule o módulo da força que o homem está aplicando, se ela for (a) paralela ao plano inclinado e se ela for (b) paralela ao piso.
A primeira coisa que devemos prestar atenção nessa questão é que o piano desliza com velocidade constante! Arrá! Isso quer dizer que não há força resultante agindo sobre ele em qualquer direção! Isso facilita (e muito) nossa vida! Por quê?
Porque quer dizer que o piano está em equilíbrio e podemos usar que
E é por essas relações que vamos resolver nosso problema.
E vamos fazer dois esquemas para entender a situação que ele descreve. No primeiro caso a força que o homem faz é paralela a rampa e depois é paralela ao piso. Fica assim:
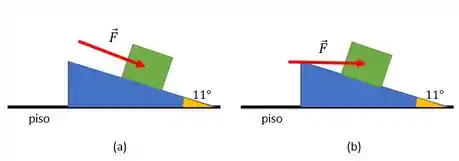
Para visualizar melhor, vamos fazer um diagrama de forças para esses dois casos e calcular a força através das equações de equilíbrio.
Vamos lá!
Passo 2
a) Caso : força aplicada sendo paralela ao plano inclinado. Vamos colocar o eixo paralelo ao plano inclinado
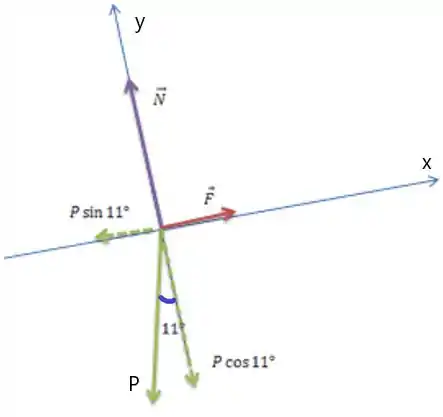
Temos que a força normal é perpendicular ao plano (eixo ) e a força peso está para baixo fazendo um ângulo de .
Como o sistema está em equilíbrio, temos na vertical,
Isolando :
Na horizontal, temos:
E isolando :
Como queremos determinar o valor de vamos usar a segunda relação:
Sendo que . Assim, temos:
Beleza? Vamos ao segundo caso?
Passo 3
b) Caso : força aplicada sendo paralela ao piso. Aqui a gente vai colocar o eixo paralelo ao piso
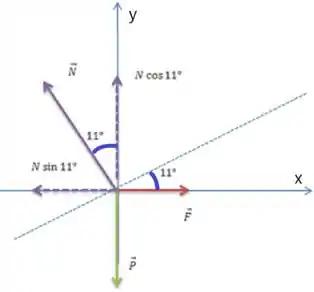
Repara que agora a força peso que é perpendicular ao plano (eixo ) e a força normal está para cima fazendo um ângulo de .
Seguindo o mesmo raciocínio para eixo , temos:
Para o eixo :
Da primeira relação podemos tirar o valor de :
E substituir na segunda para determinar o valor da força:
Calculando, obtemos:
Valeu, galera! Até a próxima! 😉