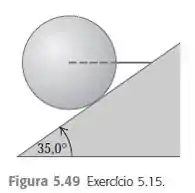
Um fio horizontal segura uma bola sólida e uniforme de massa sobre uma rampa inclinada, que forma um ângulo de acima do plano horizontal. A superfície dessa rampa é perfeitamente lisa, e o fio está direcionado para o sentido oposto ao centro da bola (Figura ).
a) Desenhe um diagrama do corpo livre para a bola.
b) Qual é a força que a superfície da rampa exerce sobre a bola?
c) Qual é a tensão no fio?
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
Nós temos uma bola sólida de massa sendo segurada por um fio em uma rampa inclinada que forma um ângulo de acima do plano horizontal. Sendo assim, ele nos pede (a) o diagrama de corpo livre da bola, (b) a força que a superfície exerce sobre a bola e (c) a tensão no fio.
Então, vamos desenhar o diagrama e usar as equações de equilíbrio obtidas da segunda de lei de Newton para calcular a força de contato da superfície e a tensão no fio .
Vamos lá!
Passo 2
Sobre a bola estão agindo a força peso (perpendicular o chão, apontando para baixo), a força tensora que segura a bola na rampa (paralela ao chão para a direita) e a normal que é sempre perpendicular à superfície de contato, nesse caso, à rampa. O diagrama de forças fica assim ó:
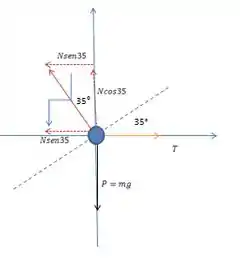
Em amarelo está a tensão, em vermelho a normal (e pontilhado suas componentes) e em preto o peso.
Passo 3
A força que a superfície da rampa exerce sobre a bola é a força normal. Como o sistema está em equilíbrio, a soma de todas as forças numa mesma direção é zero. Assim olhando na direção vertical temos:
Como a massa é e podemos calcular na forma:
Passo 4
E a tensão no fio pode ser encontrada a partir do equilíbrio de forças na direção horizontal, saca só:
Valeu, galera! Até a próxima! 😉
Resposta
a)
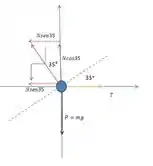
b)
c)