Uma corda leve está amarrada a um bloco com massa de , que está em repouso sobre uma superfície horizontal e sem atrito. A corda horizontal passa por uma polia sem atrito e sem massa, e um bloco com massa está suspenso na outra ponta. Quando os blocos são soltos, a tensão na corda é de .
a) Desenhe dois diagramas do corpo livre, um para o bloco de e outro para o bloco com massa.
b) Qual é a aceleração de cada bloco?
c) Ache a massa m do bloco suspenso.
d) Como a tensão se relaciona com o peso do bloco suspenso?
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
O enunciado nos diz que um bloco de massa está amarrado a uma extremidade de uma corda, repousando sobre uma superfície horizontal sem atrito. Essa corda passa por uma polia e tem um outro bloco de massa suspenso na outra ponta. Quando esses blocos são soltos, temos uma tensão na corda .
Com base nessas informações, precisamos (a) desenhar o diagrama de corpo livre para cada bloco, (b) determinar a aceleração de cada um deles, (c) encontrar a massa do bloco suspenso e (d) descobrir uma relação entre a tensão da corda e o peso do bloco suspenso.
Pra isso, vamos usar a segunda lei de Newton () para fazer o somatório das forças presentes no sistema e encontrar as nossas variáveis.
Vamos lá!
Passo 2
No bloco de massa está agindo a força peso vertical para baixo, e como ele está apoiado em uma superfície horizontal temos a força normal vertical para cima.
Essas duas forças se anulam (elas não formam par ação reação!). Outra força que está agindo sobre esse bloco é a força tensora de para a direita.
No outro bloco age a força peso para baixo e a força tensora para cima. O bloco de se movimenta para a direita enquanto que o bloco de massa se movimenta para baixo.
O diagrama para os dois blocos pode ser então desenhado assim ó:
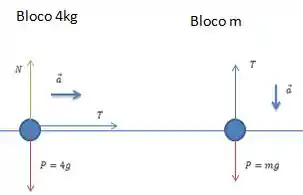
Passo 3
Para determinar a aceleração vamos aplicar a segunda lei para o bloco de na direção horizontal:
Assim, substituindo os valores da massa e da tensão na corda, temos:
Passo 4
Para achar a massa do bloco suspenso vou aplicar a segunda lei na direção vertical. Lembrando que a força de tensão é igual para todo sistema (o fio é o mesmo!) e a aceleração dos blocos deve ser igual (eles se movimentam juntos). Assim, da segunda lei, temos:
Isolando :
Substituindo os valores do enunciado:
Encontramos a massa do bloco suspenso:
Passo 5
Agora analisando o sistema, percebemos que o peso do bloco de massa deve ser maior do que a tensão. Porque se fosse o contrário esse bloco subiria e não desceria, como acontece.
Assim, vamos ter:
Logo,
Valeu, galera! Até a próxima! 😉
Resposta