No instante , um elétron que está se movendo no sentido positivo do eixo x penetra em uma região onde existem um campo elétrico e um campo magnético , com paralelo ao eixo y. A Fig. 28-32 mostra a componente y da força total exercida pelos dois campos sobre o elétron em função da velocidade v do elétron no instante . A escala do eixo horizontal é definida por . As componentes x e z da força total são zero no instante . Supondo que , determine (a) o módulo E do campo elétrico: (b) o campo magnético em termos dos vetores unitários.

Quando nosso elétron entra no campo elétrico e magnético, ambas as forças elétricas e magnéticas atuam sobre ele. Escrevemos a força total:

Escrevendo as forças, obtemos:

Usando o fato de que a velocidade inicial está direcionada ao longo do eixo , trabalhamos no produto vetorial considerando a força total e obtemos:

Inserindo isso em e usando o fato de que o campo elétrico é paralelo ao eixo , temos:

Agora, projetando a expressão anterior nos três eixos, obtemos:

Como esperado, a componente inicial da força líquida é zero.

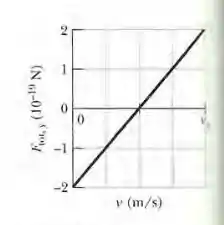
1. Para encontrar a magnitude do campo elétrico, analisaremos a expressão e usaremos a figura fornecida.

A figura mencionada é na verdade um gráfico de uma equação . Isso é um gráfico de como uma função da velocidade .

Olhando a figura nós vemos que no ponto , a coordenada da força é

Reorganizando e sabendo que

Como há apenas a componente do campo elétrico, acabamos de encontrar a magnitude desejada do campo elétrico:

(b)O gráfico da Fig. 28-32 mostra que a força total é zero quando a velocidade do elétron é .

De acordo com a Eq. 28-7 (, isso significa que