Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 49

A intensidade do campo elétrico a 5,0   c m de um eletrodo extenso e carregado é de 1 000 N C . Qual é a carga (em nC) sobre um trecho circular do eletrodo com 1,0   c m de diâmetro?

Passo 1

Faaaaaala, galera... Tranquileba??

Primeiro, definamos o campo elétrico perto de um plano onde z é muito muito maior que o raio. Assim:

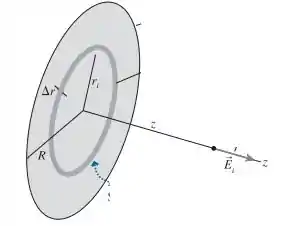
Sabemos pela definição de campo que:

E i = 1 4 π ε 0 ∫ d q r ' 2

Vemos que o campo em x e y se cancelam, logo:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ d q r ' 2 cos ⁡ θ

Sabemos que a densidade de carga é dada por:

η = q A

d q = η   d A = η d π r 2 = η 2 π r   d r

Assim:

E → =   1 4 π ε 0 ∫ η 2 π r d r r ' 2 cos ⁡ θ

Para:

r ' = r 2 + z 2 1 2

E:

cos ⁡ θ = r r ' = r r 2 + z 2 1 2

Assim ficando:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ η   2 π r d r r 2 + z 2   r r 2 + z 2 1 2 = η z 2   ε 0 ∫ r r 2 + z 2 3 2   d

Integrando de 0 ≤ r ≤ R , temos que o campo sobre um disco é:

E → = η 2 ε 0 1 - z R 2 + z 2

Para z ≫ R :

E → = η 2 ε 0 1 - 1 R 2 z 2 + 1

E = η 2 ϵ 0

Sabemos por definição que:

η = Q A

Assim:

Q A = E * 2 ϵ 0

Bora pro próximo passo comigo?

Passo 2

Pede-se Q, e sabemos que A = π r 2

π r 2 = Q E 2 ϵ 0

Q = π r 2 * E ( 2 ϵ 0 )

Passo 3

Aplicando valores:

Q = π 1 2 1 × 10 - 2 m 2 * 1000 N C 2 8.85 × 10 - 12 C 2 N m 2

Concluímos que:

Q = 1.39 × 10 - 12 C = 1.39 × 10 - 3   n C  

Resposta

Q = 1.39 × 10 - 3   n C  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Problemas de 62 a 65, uma ou várias equações lhe são fornecidas para a resolução de um problema. Em cada uma das questões, Elabore um problema realista para o qual o conjunto de equações fornecido
Mostre que o campo elétrico sobre o eixo de simetria de um anel de carga tem o comportamento esperado para z ≪ R e para z ≫R .
Mostre que a máxima intensidade de campo elétrico sobre o eixo de simetria de um anel de carga ocorre em z = R 2 Qual é a intensidade do campo elétrico neste ponto?
Suponha que você segure duas grandes folhas de plástico frente à frente, espaçadas uma da outra por d, conforme mostra a FIGURA P27.48. Atritando uma delas com lã e a outra com seda, você consegue obt
Você conseguiu um emprego em uma companhia que projeta e constrói nanomáquinas. Um engenheiro da empresa está projetando um oscilador microscópico para ajudar a medir o tempo, e você foi indicado para