Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 45

  1. Mostre que a máxima intensidade de campo elétrico sobre o eixo de simetria de um anel de carga ocorre em z = R 2
  2. Qual é a intensidade do campo elétrico neste ponto?

Passo 1

Faaaaaala, galera... Tranquileba??

Primeiro precisamos saber qual o campo elétrico no eixo de simetria de um anel. Bora lá?!

Temos então:

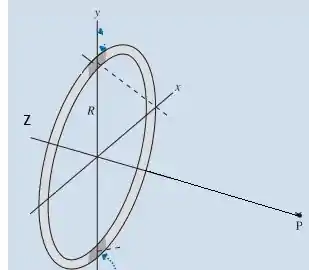
E pede-se então o campo. Bom, sabemos que as componentes em y e x se anulam existindo assim somente componentes em z. logo:

E z = E i cos i ⁡ θ = 1 4 π   ε 0   Δ Q r i 2 cos i ⁡ θ             ( 0.1 )

Sendo r i o modulo da distancia do ponto a um ponto quaisquer do bastão, assim:

r i 2   = z 2 + R 2

E R a distancia ao raio do bastão.

E sabemos também que:

cos i ⁡ θ = z z 2 + R 2

De modo que:

E z = 1 4 π   ε 0   Δ Q z 2 + R 2 z z 2 + R 2 = 1 4 π   ε 0 z     Δ Q z 2 + R 2 3 2  

Como o campo elétrico está em Z e não há componente da carga na linha z, z é constante. Logo

E z = 1 4 π   ε 0 z     z 2 + R 2 3 2   ∫ d Q

E como a soma da carga é a carga:

E z = 1 4 π   ε 0 z     z 2 + R 2 3 2   ∫ 0 Q d Q = 1 4 π   ε 0 z   Q   z 2 + R 2 3 2  

Portanto:

E a n e l = 1 4 π   ε 0   z   Q   z 2 + R 2 3 2

E para acharmos o ponto máximo em z usamos o que o bom e velho Cálculo nos diz:

d E d z = 0

Assim acharemos no próximo passo. Vem comigo?!

Passo 2

Deste modo:

d E a n e l d z = Q 4 π ϵ 0   d d z z z 2 + R 2 3 2 = 0

Q 4 π ϵ 0 1 z 2 + R 2 3 2 - 3 z 2 z 2 + R 2 5 2 = 0

Então:

1 z 2 + R 2 3 2 - 3 z 2 z 2 + R 2 5 2 = 0

1 z 2 + R 2 3 2 = 3 z 2 z 2 + R 2 5 2  

1 = 3 z 2 z 2 + R 2

2 z 2 = R 2

∴ z = R 2

Portanto o campo elétrico será máximo quando z = R 2

Passo 3

Para b)

Temos:

E a n e l = 1 4 π   ε 0   z   Q   z 2 + R 2 3 2

Fazendo z = R 2

E m á x i m o = 1 4 π   ε 0   R 2   Q   R 2 2 + R 2 3 2

E m á x i m o = 2 3 3   Q 4 π ϵ 0 R 2

Resposta

Para b)

E m á x i m o = 2 3 3   Q 4 π ϵ 0 R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um anel com raio a está no plano z = 0 com seu centro na origem. O anel está uniformemente carregado e tem uma carga total Q . Determine E z no eixo z em (a) z = 0,2 a , (b) z = 0,5 a , (c) z = 0,7 a
Um disco não condutor de raio a está no plano z = 0 com seu centro na origem. O disco está uniformemente carregado e tem uma carga total Q . Determine E z no eixo z em em (a) z = 0,2 a , (b) z = 0,5 a
Usando uma planilha eletrônica ou uma calculadora gráfica faça um gráfico da intensidade do campo elétrico no eixo de um disco que tem um raio a = 3,00c m e uma densidade superficial de carga σ = 0,50
Um bastão plástico não condutor, fino e longo, é dobrado para formar uma circunferência de raio a . Entre as extremidades do bastão permanece um pequeno espaçamento de comprimento l , onde l ≪ a . Uma
Um anel uniformemente carregado tem um raio a , está um plano horizontal e tem carga negativa - Q . Uma pequena partícula está localizada no eixo do anel. (a) Qual é o mínimo valor de q / m tal que a