Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 40

40- Um capacitor de 12.4   μ F é conectado através de um resistor de 0.895   M Ω a uma diferença de potencial constante de 60.0   V .

( a ) Calcule a carga do capacitor nos seguintes instantes depois que a conexão é feita: 0 ; 5.0   s ; 10.0   s ; 20.0   s e 100.0   s

( b ) Calcule as correntes de carga do capacitor nos mesmos instantes.

( c ) Faça um gráfico para os itens ( a ) e ( b ) para t entre 0 e 20   s .

Passo 1

A carga no capacitor pode ser vista na Equação ( 26.12 ) na página 183 da edição 5 desse livro e é:

q = C ϵ 1 - e - t R C

Onde C = 12.4 × 10 - 6   F ,   R = 0.895 × 10 6 e ϵ = 60   V , então para um tempo t (em segundos) nós teremos uma carga de:

t = 0 ; q = 12.4 × 10 - 6 × 60 1 - e 0 = 0   C

t = 5 ; q = 12.4 × 10 - 6 × 60 1 - e -   5 0.895 × 10 6 × 12.4 × 10 - 6 = 2.7 × 10 - 4   C

t = 10 ; q = 12.4 × 10 - 6 × 60 1 - e -   10 0.895 × 12.4 = 4.42 × 10 - 4   C

t = 20 ;   q = 12.4 × 10 - 6 × 60 1 - e -   2 0 0.895 × 12.4 = 6.21 × 10 - 4   C

t = 100 ;   q = 12.4 × 10 - 6 × 60 1 - e -   10 0 0.895 × 12.4 = 7.44 × 10 - 4   C

Passo 2

Já a corrente d q / d t é vista na equação ( 26.13 ) e será:

i = ϵ R   e - t R C

E para os mesmos instantes do passo anterior nós temos:

t = 0 ; i = 60 0.895 × 10 6   e - 0 0.895 × 12.4 = 6.7 × 10 - 5   A

t = 5 ; i = 60 0.895 × 10 6   e - 5 0.895 × 12.4 = 4.27 × 10 - 5   A

t = 1 0 ; i = 60 0.895 × 10 6   e - 1 0 0.895 × 12.4 = 2.72 × 10 - 5   A

t = 2 0 ; i = 60 0.895 × 10 6   e - 2 0 0.895 × 12.4 = 1.11 × 10 - 5   A

t = 10 0 ; i = 60 0.895 × 10 6   e - 10 0 0.895 × 12.4 = 8.19 × 10 - 5   A

Passo 3

O gráfico da carga no capacitor é:

q = 7.44 × 10 - 4 1 - e - t 11.098

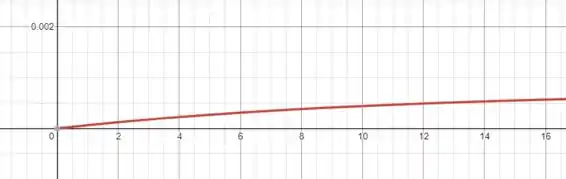
Já para a corrente temos:

i = 6.704 × 10 - 5   e - t 11.098

Quando o circuito começa a carga no capacitor é nula e a corrente é máxima, e a medida que o capacitor vai enchendo a corrente tende a ser nula.

Resposta

a )   t = 0 ; q = 0   C

t = 5   s ; q = 2.7 × 10 - 4   C

t = 10   s ; q = 4.42 × 10 - 4   C

t = 20   s ; q = 6.21 × 10 - 4   C

t = 100   s ; q = 7.44 × 10 - 4   C

b )   t = 0 ; i = 6.7 × 10 - 5   A

t = 5   s ;   i = 4.27 × 10 - 5   A

t = 10   s ; i =   2.72 × 10 - 5   A

t = 20   s ; i =   1.11 × 10 - 5   A

t = 100   s ;   i = 8.19 × 10 - 5   A

c )   G r á f i c o s   d o   P a s s o   3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Obtenha a energia total dissipada no resistor durante esse tempo. Mostre que a metade da energia fornecida estará armazen
No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Ache a corrente I em função do tempo.
No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Ache a energia armazenada em C , após um tempo muito longo.
No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado. Demonstre que, após um tempo muito longo, metade da energia fornecida pela bateria estará armazenada no capacitor, e a o
No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Ache a energia total fornecida pela bateria, durante esse tempo.