Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 3
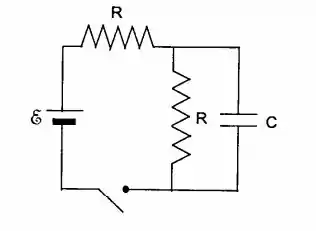
No circuito da figura, a chave é ligada para , com o capacitor descarregado. Calcule a voltagem através do capacitor após um tempo .
Passo 1
Para resolvermos, vamos utilizar as leis de Kirchoff para circuitos em série e paralelo, somando as tensões de todo o sistema. Com isso, vamos encontrar nossa corrente que passa pelo capacitor, aí aplicaremos a seguinte relação
Para encontrarmos a carga que passa pelo capacitor. Após isso, tudo que teremos que fazer é dividir pela capacitância para encontrar a tensão que passa pelo capacitor.
Passo 2
Bom, vamos lá! Como já dito no passo 1, vamos começar montando a distribuição da tensão pelo circuito, já que temos parte em série e parte em paralelo. Temos que toda a tensão que passa pelo sistema é
Como a segunda resistência está em paralelo, precisamos antes encontrar o valor da corrente que passa por ela. Podemos escrever outra equação para esse circuito, que é:
Com essa equação, chegamos que . Substituindo na nossa primeira, vamos ter que:
Se derivarmos essa relação, vamos ter que
E como já vimos no capitulo, . Substituindo e manipulando, vamos ter que
Integrando de até , onde , vamos ter que
Como queremos a tensão no capacitor, precisamos aplicar que . Assim, integrando de até , vamos chegar que
Dividinco pela capacitância, vamos chegar no nosso resultado, que é