Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 88
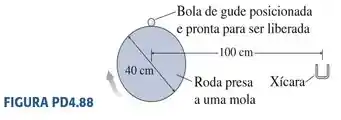
88. Um brinquedo comum de parque de diversões, ilustrado na FIGURA PD4.88, é capaz de lançar uma bola de gude em direção a uma pequena xícara. A bolinha, inicialmente em repouso sobre um grampo, é posicionada logo acima do topo de uma roda que está presa a uma mola espiral enrolada. Ao ser liberada, a roda passa a girar em sentido horário e com aceleração angular constante, abrindo o grampo e liberando a bola de gude após completar de revolução. Que aceleração angular é necessária para que a bolinha aterrisse dentro da xícara?
Passo 1
Opa! Aqui vamos nós pro nosso último problema desse capítulo!
Olha só! A nossa bolinha segue a seguinte trajetória descrita na figura abaixo...
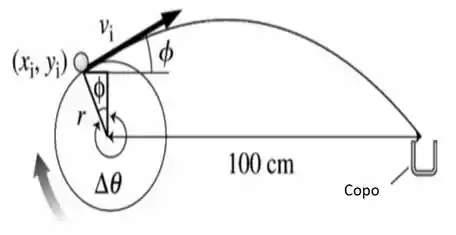
E por essa figura e o que tiramos do enunciado, sabemos que...
Onde é a notação pra inicial e é a notação pra final.
Quanto às acelerações, temos apenas a presença da gravidade atuando. Desse modo,
Já quanto às velocidades tanto angulares como linear...
E por último, em relação à variação de ângulo ...
Pronto! Temos todos os dados que precisávamos.
Passo 2
Agora vamos começar nossa resolução!
A velocidade inicial do projétil é a velocidade tangencial no ponto de liberação e a direção é tangencial à roda. A estratégia é encontrar a velocidade inicial e em seguida, usar para encontrar a aceleração angular necessária
Como o ponto de liberação está em um ângulo de...
Então, o valor de vai ser...
No sistema de coordenadas da figura, obtemos assim, que:
Passo 3
Quanto ao ângulo de lançamento ... Este é identificado calculando os ângulos no triângulo retângulo destacado na figura e percebendo que a velocidade inicial é tangencial ao círculo. Assim, o ângulo de lançamento também é .
Desse modo, vamos usar a Equação para a posição de um projétil em função do tempo, e usaremos o fato de que o tempo para percorrer a distância horizontal até o copo é o mesmo para o movimento vertical. Para isso... Primeiro, é importante encontrar o tempo de vôo necessário para a bola atingir o copo com o movimento horizontal;
Substitundo esse tempo na equação do movimento vertical...
E para obter a velocidade angular inicial, basta dividir essa velocidade pelo raio...
Passo 4
Pra finalizar, basta usar a equação de sabendo que a velocidade angular inicial é nula...
Essa aceleração angular na verdade equivale à...
E pronto! Obtemos nossa resposta! Essa era a aceleração angular necessária!