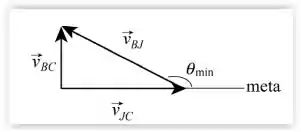
Um jogador de rúgbi corre com a bola em direção à meta do adversário, no sentido positivo de um eixo . De acordo com as regras do jogo, pode passar a bola a um companheiro de equipe desde que a velocidade da bola em relação ao campo não possua uma componentex positiva. Suponha que o jogador esteja correndo com uma velocidade de em relação ao campo quando passa a bola com uma velocidade em relação a ele mesmo. Se o módulo de é , qual é o menor ângulo que a bola deve fazer com a direção x para que o passe seja válido?

Então galera , a primeira coisa que devemos fazer é atribuir nomes aos componentes do problema ,para não ficarmos perdidos depois .Chamamos a velocidade do jogador em relação ao campo de e a velocidade relativa da bola em relação ao jogador de . Nesse caso, a velocidade da bola em relação ao campo é dada por . O menor ângulo, , corresponde ao caso em que . Assim,