Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.7 - Ex. 67
Um menino faz uma pedra descrever uma circunferência horizontal com de raio e uma altura de acima do chão. A corda arrebenta e a pedra é arremessada horizontalmente, chegando ao solo depois de percorrer uma distância horizontal de . Qual era o módulo da aceleração centrípeta da pedra durante o movimento circular?
Passo 1
Show de bola pessoal, bora dar uma olhadinha na ilustração do problema pra visualizarmos melhor :
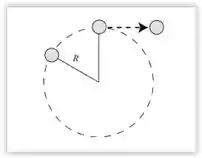
Reparem que pedra está descrevendo inicialmente um movimento circular uniforme, mas passa a descrever uma trajetória balística (lançamento horizontal) depois que a corda arrebenta . Como , para calcular a aceleração centrípeta da pedra, precisamos conhecer a velocidade escalar durante o movimento circular, que é também a velocidade inicial do movimento balístico quando a corda arrebenta. Sendo assim, samos as equações do movimento balístico para calcular essa última velocidade.
Até aqui tranquilo? Vamos continuar então!
Passo 2
Belezoca, é sempre importante nesse tipo de exercício definir a direção que cada eixo representada , nesse caso , escolhendo o sentido do semieixo positivo como sendo para cima e a origem no ponto em que a pedra deixa de descrever o movimento circular, as coordenadas da pedra durante o movimento balístico são dadas por:
Nós sabemos que a pedra chega ao solo no ponto .
Isolando na equação da componente do deslocamento, obtemos que:
Agora bora substituir esse valor na primeira equação:
Assim, o módulo da aceleração centrípeta será:
Tal que: