Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.5 - Ex. 40

O piloto de um avião deseja voar de leste para oeste. Um vento de 80,0 km/h (sobre 50 mi/h) sopra do norte para o sul. a) Se a velocidade do avião em relação ao ar (sua velocidade se o

ar estivesse em repouso) é igual a 320,0 km/h (sobre 200 mi/h), qual deve ser a direção escolhida pelo piloto? b) Qual é a velocidade do avião em relação ao solo? Ilustre sua solução com um diagrama vetorial.

Passo 1

Fala aí! tudo certinho?

Nesse problema temos um piloto de um avião que deseja voar de leste para oeste, porém, um vento de 80,0 km/h (sobre 50 mi/h) sopra do norte para o sul. A partir daí se a velocidade do avião em relação ao ar é igual a 320,0 km/h (sobre 200 mi/h), qual deve ser a direção escolhida pelo piloto e qual é a velocidade do avião em relação ao solo.

Tem ideia de como fazemos isso?

As velocidades relativas são:

a velocidade do avião em relação ao solo: v → P / S

a velocidade do avião em relação ao ar: v → P / A = 320 k m / h

a velocidade do ar em relação ao solo: v → A / S = 80 k m / h

v → P / S deve ser para Oeste e v → A / S para o sul.

E por adição:

v → P / S = v → P / A + v → A / S

E o diagrama de adição de velocidade relativa é dado por:

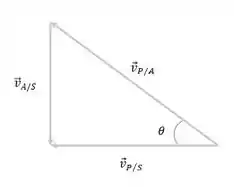
Bora lá!

Passo 2

  1. Para sabermos qual deve ser a direção escolhida pelo piloto, fazemos:

    2. sen ⁡ θ = v → A / S v → P / A = 80 k m / h 320 k m / h

    ⇒ θ = sen - 1 ⁡   80 k m / h 320 k m / h = 14 °        

    Para o norte do oeste.

    Tranquilo até aqui?

    Passo 3

  2. E calculamos o modulo da velocidade fazendo:

v → P / S = ( v → P / A ) 2 - ( v → A / S ) 2 = ( 320 k m / h ) 2 + ( 80 k m / h ) 2 = 310 k m / h

Para viajar para oeste, a velocidade do avião em relação ao ar deve ter um componente para oeste e também um componente que fica para o norte, oposto à direção do vento.

E aí! o que achou? Responde Aí!

Resposta

  1. θ = 14 ° para o norte do oeste.
  2. v → P / S = 310 k m / h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois navios, A e B , deixam o porto ao mesmo tempo . O navio A navega para noroeste a 24 nós e o navio B navega a 28 nós em uma direção 40 ° a oeste do sul. ( 1 nó =1 milha marítima por hora; veja o A
Voos longos em latitudes médias no Hemisfério Norte encontram a chamada corrente de jato, um fluxo de ar para leste que pode afetar a velocidade do avião em relação à superfície da Terra. Se o piloto
Na Fig.4-48a, um trenó se move no sentido negativo do eixo x com uma velocidade escalar constante v t , quando uma bola de gelo é atirada do trenó com uma velocidade v → 0 = v 0 x i ^ + v 0 y j ^ em r
Uma mulher que é capaz de remar um barco a 6,4k m / h em águas paradas se prepara para atravessar um rio retilíneo com 6,4k m de largura e uma correnteza de 3,2k m / h . Tome i ^ perpendicular ao rio
Um rio de 200m de largura corre para leste com uma velocidade constante de 2,0m / s . Um barco com uma velocidade de 8,0m / s em relação à água parte da margem sul em uma direção 30 ° a oeste do norte