Em um jogo de futebol, a bola está inicialmente no centro do campo. Considere um sistema de coordenadas no plano do campo e cujo centro coincida com o centro do campo. Depois do primeiro chute, a bola se encontra na posição , onde as unidades são em metros. Determine: a) o módulo do deslocamento inicial da bola; b) o ângulo entre este vetor e o eixo .

E aí galera, tudo beleza?

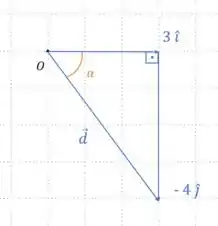
Para fazer essa questão, primeiro, vamos desenhar em uma malha quadriculada o vetor posição da bola. Inserimos os vetores componentes e depois traçamos o vetor deslocamento da bola passando pelo centro do nosso sistema, como nas figuras abaixo.

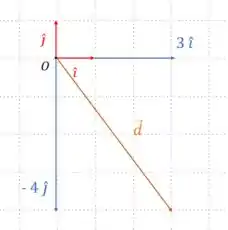
Vamos calcular o módulo do deslocamento da bola.

Perceba que transladando o vetor para a direita formamos um triângulo retângulo. Observe a figura abaixo.

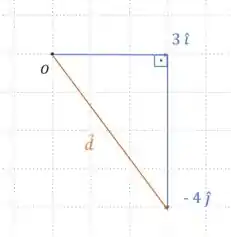
Esse triângulo também é pitagórico. Note que seus catetos medem 3 e 4, portanto o tamanho de sua hipotenusa, ou seja, o módulo do vetor deslocamento é 5.