Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.Problemas Adicionais - Ex. 49

Uma partícula sofre três deslocamentos sucessivos em um plano: d → 1 ,   4,00   m para sudoeste, d → 2 ,   5,00   m para leste e d → 3 ,   6,00   m em uma direção 60,0 ° no norte do leste. Use um sistema de coordenadas com o eixo y apontando para o norte e o eixo x apontando para o leste. Determine (a) a componente x e (b) a componente y de d → 1 . Determine (c) a componente x e (d) a componente y de d → 2 . Determine (e) a componente x e (f) a componente y de d → 3 . Considere o deslocamento total da partícula após os três deslocamentos. Determine (g) a componente x , (h) a componente y (i) o módulo e (j) a orientação do deslocamento total. Para que a partícula volte ao ponto de partida (k), que distância deve percorrer e (l) em que direção deve se deslocar?

Passo 1

Belezoca galerinha, pra ficar mais bonitinho pra gente, podemos desenhar esses deslocamentos no plano, tal que:

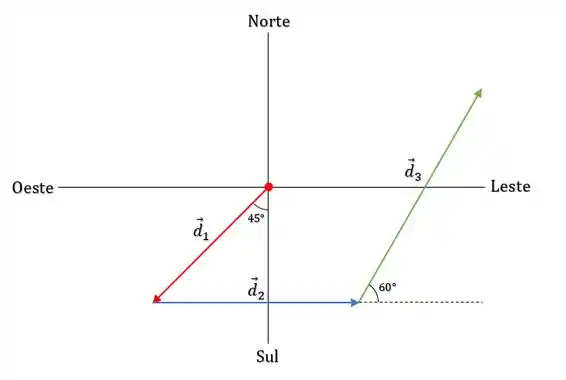
Sendo assim, podemos definir as componentes de cada deslocamento. Pra d → 1 obtemos que:

d → 1 = - 5 , 00 sen ⁡ 45 °     i ^ - 5 , 00 cos ⁡ 45 °   j ^

d → 1 = - 2,83   i ^ - 2,83   j ^

Para d → 2 temos:

d → 2 = 5,00   i ^ + 0   j ^

E para d → 3 vamos ter que:

d → 3 = 6,00 cos ⁡ 60 °   i ^ + 6,00 cos ⁡ 60 °   j ^

d → 3 = 3,00   i ^ + 5,20   j ^

Passo 2

Agora o deslocamento total, vai ser a soma de todos os deslocamentos, tal que:

d → = d → 1 + d → 2 + d → 3

Tal que:

d → = - 2,83   i ^ - 2,83   j ^ + 5,00   i ^ + 0   j ^ + 3,00   i ^ + 5,20   j ^

d → = 5,17   i ^ + 2,37   j ^

O módulo será:

d = 5,17 2 + 2,37 2

d = 5,69   m

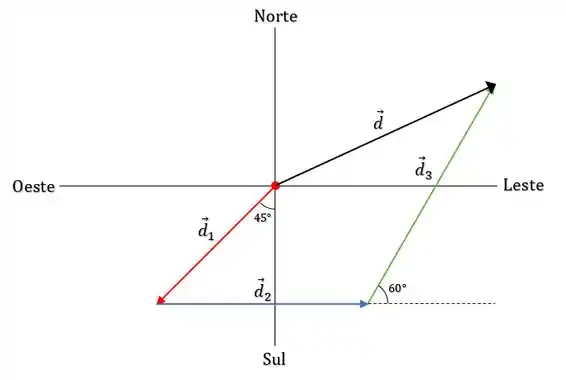
Passo 3

Agora a orientação desse deslocamento vai ser dada pelo ângulo θ que o deslocamento faz com a horizontal:

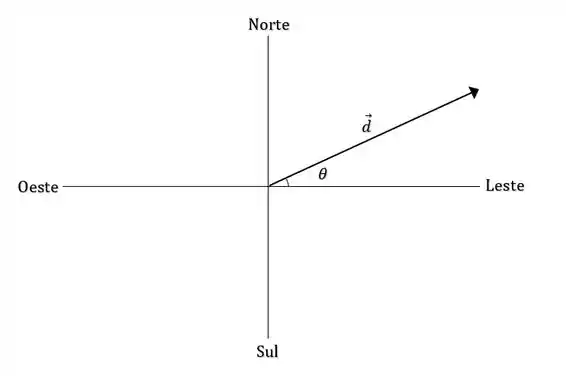
Esse ângulo pode ser dado através da relação:

tan ⁡ θ = d y d x

Logo:

θ = arctan ⁡ d y d x

θ = arctan ⁡ 2,37 5,17

θ = 25,0   °

Passo 4

E para voltar ao ponto de origem, é preciso percorrer os mesmos 5,69   m , só que dessa vez no sentido oposto ao do deslocamento.

Resposta

  1. - 2,83   m
  2. - 2,83   m
  3. 0   m
  4. 5,00   m
  5. 3,00  m
  6. 5,20   m
  7. 5,17   m
  8. 2,37   m
  9. 5,69   m
  10. θ = 25 °   ao norte do oeste
  11. 5,69 m
  12. θ = 25 °   ao sul do oeste
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se d 1 →=3 i →- 2 j →+ 4 k → e d 2 →=- 5 i →+ 2 j →– k → , determine d → 1 +d → 2 . d → 1 × 4 d → 2 .
O vetor posição de um elétron é r →=5,0m i →-3,0m j →+2,0m k → . (a) Determine o módulo de r → . (b) Desenhe o vetor em um sistema de coordenadas dextrogiro.
Duas cordas em um plano vertical exercem as mesmas forças de módulo sobre um peso suspenso, mas a tração entre elas possui um ângulo de 86,0 ° . Qual é a força de tração que cada uma exerce, se a traç
Use componentes de vetores para determinar o módulo e a direção do vetor necessários para equilibrar os dois vetores demonstrados na Figura 1.36. Considere o vetor 625 - N ao longo do eixo – O y e con
Uma formiga, enlouquecida pelo Sol em um dia quente, sai correndo em um plano x y . As componentes ( x e y ) de quatro corridas consecutivas em linha reta são as seguintes, todas em centímetros: 30,0