Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.4 - Ex. 4
Na Fig. 3-27, uma máquina pesada é erguida com o auxílio de uma rampa que faz um ângulo com a horizontal, na qual a máquina percorre uma distância . (a) Qual é a distância vertical percorrida pela máquina? (b) Qual é a distância horizontal percorrida pela máquina?
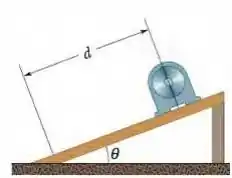
Passo 1
Para esta questão podemos usar diretamente a ilustração para nos auxiliar na interpretação.
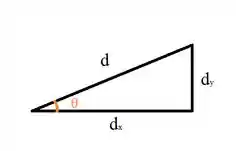
Com este triângulo retângulo definido podemos determinar as componentes verticais e horizontais através da trigonometria.
Passo 2
Pela definição de cosseno:
Substituindo os valores de e temos:
Isolando , determinamos o deslocamento horizontal:
Passo 3
Aplicando agora a definição do seno:
Substituindo os valores de e , temos:
Isolando determinamos o deslocamento vertical:
Resposta
Exercícios de Livros Relacionados
O objetivo de um navio échegar a um porto situado 120k m ao norte do ponto de partida, mas uma tempestade inesperada o leva para um local situado 100k m a leste do ponto de partida. (a) Que distância
Quais são (a) a componente x e (b) a componente y de um vetor a → do plano x y que faz um ângulo de 250 ° no sentido anti-horário com o semieixo x positivo e tem um módulo de 7,3m ?
Um vetor deslocamento r → no plano x y tem 15m de comprimento e faz um ângulo θ = 30 ° com o semieixo x positivo, como mostra a Fig 3-26. Determine (a) a componente x e (b) a componente y do vetor.
As dimensões de uma sala são 3,00m (altura) X 3,70m X 4,30m . Uma mosca parte de um canto da sala e pousa em um canto diagonalmente oposto. (a) Qual é o módulo do deslocamento da mosca? (b) A distânci
A componente x do vetor A → é - 25,0m e a componente y é + 40,0m . (a) Qual é o módulo de A → ?(b) Qual é o ângulo entre a orientação de A → e o semieixo x positivo?