Em um jogo de sinuca, a tacadeira, que tem uma rapidez inicial de , sofre uma colisão elástica com a bola oito, que está inicialmente em repouso. Após a colisão, a bola oito se move formando um ângulo de à direita da orientação original da tacadeira. Suponha as bolas com massas iguais. (a) Determine a orientação do movimento da tacadeira imediatamente após a colisão. (b) Determine a rapidez de cada bola imediamente após a colisão.
Passo 1
a) Olá, tudo bem?
Então, essa tacadeira é a bolinha branca da sinuca. Ele diz que ela foi jogada com rapidez de e atingiu a bola 8, que depois da colisão, se move sem um ângulo de a direita da orientação em que a tacadeira foi jogada. Vamos fazer um esqueminha.
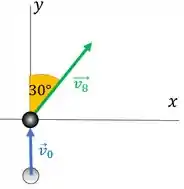
A gente só assumiu que está na direção para ter um referencial, tá?
E a primeira coisa que ele quer saber é a orientação da bolinha branca depois da colisão. Que a gente pode interpretar como o ângulo da velocidade final da bolinha com o vetor . Vamos ver como achar isso!
Passo 2
Como ele diz que a colisão é elástica, podemos afirmar que a energia cinética se conservou na colisão. Ou seja,
A energia cinética inicial é dada apenas pela bola branca, já que a bola 8 está em repouso no começo. Então temos
Depois a energia cinética é dada pelas duas bolas em movimento. O enunciado diz que elas têm a mesma massa . E a gente pode considerar que a rapidez depois da colisão da tacadeira é e da bola 8 é . A energia cinética final fica:
Aí a conservação de energia fica:
Passo 3
Simplificando o que a gente achou:
Essa relação parece muito com o teorema de Pitagoras, né? É porque é mais ou menos isso mesmo, mas com os vetores das velocidades. A ideia é que o vetor velocidade inicial da bola branca pode ser a hipotenusa de um triângulo, onde os catetos são e . Tipo assim:
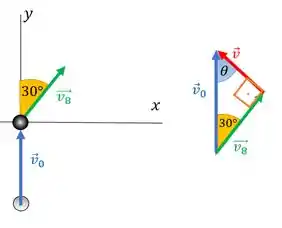
Outra forma de a gente interpretar isso, é que, como as massas das bolinhas são iguais, para haver a conservação de energia, a velocidade inicial da bola branca precisa ser igual a soma vetorial das velocidades finais das duas bolas.
Por isso nosso triângulo tem cara de soma vetorial. E o que a gente queria? A orientação de , a velocidade final da bola branca. A soma de ângulos internos do triângulo é , então para achar o ângulo que faz com (com a direção de ), a gente faz
Passo 4
b) Queremos a rapidez de cada bolinha. Mas percebe que a gente tem um movimento em duas dimensões. Então a gente pode montar a equação de conservação de quantidade de movimento para cada um direção que a gente tem: e .
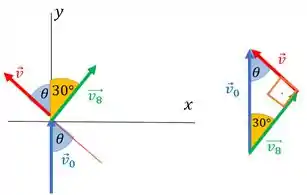
Agora vamos usar conservação da quantidade de movimento no eixo y:
As componentes de e vão usar o cosseno do ângulo que orienta esses vetores, porque ambos os ângulos estão colados em . E a componente de vai ser mesmo porque ela está na vertical. Ficamo assim:
Cortando a massa e substituindo os valores do ângulo e da velocidade inicial:
Passo 5
E conservando a quantidade de movimento no eixo x:
Aqui a gente vai usar seno para as componentes de e . Mas repara que aponta para a parte negativa de , então fica com sinal de menos. E é nula, já que é vertical. Então temos:
Cortando a massa e substituindo os valores dos ângulos:
Botando isso na equação :
Daí, achamos voltando em :
Resposta
Velocidade da tacadeira:
Velocidade da bola 8: