Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 56
Uma pequena bola de borracha, de massa , se move com rapidez para a direita, de encontro a um taco muito mais massivo, que se desloca para a esquerda com rapidez. Determine a velocidade da bola após ela sofrer uma colisão frontal elástica com o taco.
Passo 1
Mais uma questãozinha de colisões! Como aqui não falamos da massa dos corpos, mas só das velocidades deles, a gente vai ter que lembrar do coeficiente de restituição, que relaciona a velocidade relativa dos corpos antes e depois. Não esquece: na colisão elástica, o coeficiente de restituição vale 1. Vamos dar uma olhada em como podemos aplicar isso.
Passo 2
O coeficiente de restituição é dado por:
Vamos chamar as velocidades do taco e da bola de e de , e adotar o sentido positivo para a direita.
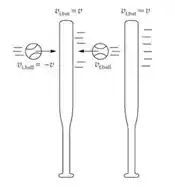
Antes, eles estavam se aproximando. Nesse caso, a velocidade relativa era dada por:
Depois do choque, eles vão se afastar, mas no mesmo sentido para a esquerda. A velocidade relativa é:
O sinal do é negativo pois está no sentido para a esquerda.
Como a massa do taco é muito maior que a da bola, podemos considerar que sua velocidade não mudou com o choque. Assim, Daí, substituindo na fórmula do coeficiente de restituição:
Ou seja, a bola passa a se mover com velocidade para a esquerda.
Resposta
A velocidade da bola vai ser para a esquerda.