Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 87

Um disco de 5,0 k g de massa, movendo-se a 2,0 m / s , se aproxima de um disco idêntico que está estacionário sobre o gelo, sem atrito. Após a colisão, o primeiro disco emerge com uma rapidez v 1 → formando 30 ° com sua orientação original de movimento. O segundo disco emerge com uma rapidez v 2 → a 60 ° , como na figura. (a) Calcule v 1 → e v 2 → . (b) A colisão foi elástica?

Passo 1

Vamos lá!! A gente tem um disco de massa m = 5,0   k g se movendo em velocidade v i → = 2,0   m / s , encontra um outro disco idêntico, mas esse se encontra parado e o que o problema ta pedindo pra a gente é pra a gente achar as novas velocidades v 1 e v 2 !

A gente tem esse esqueminha aqui:

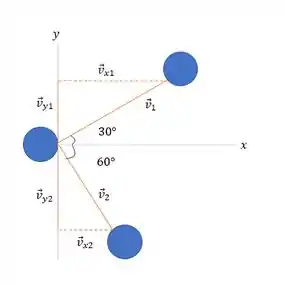
Para achar as velocidades v 1 e v 2 vamos usar a conservação de quantidade de momento no eixo x e no eixo y , mas para isso primeiro a gente tem que decompor as velocidades!

Começando por v 1 :

v → x 1 = v 1 sin ⁡ 90 ° - 30 °

v → y 1 = v 1 cos  ⁡ 90 ° - 30 °

Agora v → 2 :

v → x 2 = v 2 sin ⁡ 90 ° - 60 °

v → y 2 = v 2 cos  ⁡ 90 ° - 60 °

Passo 2

A conservação da quantidade de movimento no eixo x : fica:

m v → 0 x = m v 1 sin ⁡ 90 ° - 30 ° + m v 2 sin ⁡ 90 ° - 60 °

Como a massa dos discos são iguais:

v → 0 x = v 1 sin ⁡ 60 ° + v 2 sin ⁡ 30 °

O problema diz que v → 0 x = 2   m / s :

2 = v 1 sin ⁡ 60 ° + v 2 sin ⁡ 30 °

Calculando os senos:

2 = 3 2 v 1 + 1 2 v 2

Isolando v 1 :

v 1 = - v 2 + 4 3

Passo 3

Agora para o eixo y , já vamos escrever sem a massa porque a gente já viu que da pra cortar:

v → 0 y = v 1 cos  ⁡ 90 ° - 30 ° + - v 2 cos  ⁡ 90 ° - 60 °

O disco inicialmente só se move na direção x , logo v → 0 y = 0 , substituindo e resolvendo os cossenos:

0 = 1 2 v 1 - 3 2 v 2

Isolando v 1 :

v 1 = 3 v 2

Passo 4

Agora a gente pode igualar v 1 que encontramos nos passos 3 e 4 :

v 1 = - v 2 + 4 3

v 1 = 3 v 2

Igualando:

- v 2 + 4 3 = 3 v 2

Isolando v → 2 :

v 2 = 4 3 3 + 1 = 4 4 = 1

v 2 = 1 m / s

Agora que conhecemos v 2 podemos achar v 1 :

v 1 = 3 v 2 = 3 × 1

v 1 = 1,73   m / s

Passo 5

Agora a gente quer saber se a colisão é elástica ou não! Para isso precisamos usar a equação de energia!

E c = m v 2 2

A energia cinética antes e depois da colisão devem ser iguais:

m 1 i v 1 i 2 2 = m 1 f v 1 f 2 2 + m 2 f v 1 f 2 2

Como as massas são iguais, podemos simplificar essa expressão:

v 1 i 2 = v 1 f 2 + v 1 f 2

Temos todos os valores, então vamos calculado do lado direito e esquerdo e ver se confere:

2 2 = 1,73 3 + 1 2

4 = 4

Logo, a colisão é sim elástica!!

Resposta

  1. v 1 = 1.73 m / s e v 2 = 1.0 m / s
  2. A colisão é elástica.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para explicar a resistência do ar (mais geralmente, de qualquer fluido) ao movimento de um corpo através dele, Newton propôs o seguinte modelo. O fluido é imaginado como sendo composto de um grande nú
Calcule a magnitude (em kgf ) da força impulsiva que atua em cada um dos exemplos seguintes: (a) Num saque de jogo de tênis, a bola, de massa igual a 60g , é lançada com uma velocidade de 40m/s; o tem
Considere a colisão elástica entre duas partículas de massas m 1em 2 que se movem em uma dimensão. (a) Verifique, a partir das (9.4.11), que a velocidade do CM se conserva na colisão. (b) Calcule as v
O espalhamento elástico de um próton por um núcleo alvo desconhecido em repouso é observado numa câmara de bolhas, onde existe um campo magnético perpendicular ao plano de movimento do próton. Verific
Na teoria corpuscular da luz, no século 17, imaginava-se um feixe de luz como constituído de corpúsculos muito pequenos, movendo-se com velocidade muito elevada. A reflexão da luz num espelho seria pr