Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 78

José, cuja massa é de 75   k g , acabou de completar seu primeiro salto de bungee jump e agora está oscilando para cima e para baixo preso à extremidade da corda. Suas oscilações têm amplitude inicial de 11,0   m e período de 4,0   s .

  1. Qual é a constante elástica da corda de bungee jump?
  2. Qual é o valor máximo da velocidade de José durante as oscilações?
  3. De que altura acima do ponto mais baixo das oscilações José saltou?
  4. Se a constante de amortecimento devido à resistência do ar for de 6.0   k g / s , quantas oscilações José efetuará antes que sua amplitude se reduza a 2,0   m ?

Dica: Embora não seja inteiramente realista, considere a corda de bungee jump como se fosse uma mola ideal que tanto pode ser comprimida para reduzir seu comprimento como pode ser esticada para aumentar seu comprimento.

Passo 1

Se liga! Para resolver o item (a) precisamos usar que o período de oscilação é dado por

T = 2 π m k

Logo

k = m 2 π T 2

Substituindo os valores dados no enunciado, temos

k = 75 2 π 4 2 = 185   N / m     .

Passo 2

No item (b), o enunciado pede a velocidade máxima atingida. A expressão para a velocidade máxima é

v m a x = ω A

Como

ω = 2 π T = 2 π 4   r a d / s

podemos substituir e achar a solução como

v m a x = 2 π 4 × 11 = 17,3   m / s .

Passo 3

No item (c) o enunciado pede a altura, em relação ao ponto mais baixo da trajetória, que José pulou.

Considerando que a oscilação ocorre em torno do ponto de equilíbrio, podemos achar esse deslocamento da mola.

k x - m g = 0

x = m g k = 75 × 9,8 185 = 3,97   m

Agora podemos usar a conservação da energia.

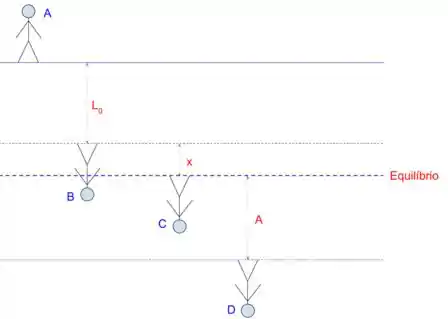
Tomando a posição de equilíbrio como h = 0 podemos dizer que em A a energia do sistema é

E A = U A = m g L 0 + x   .   ( 1 )

Como a posição B representa o instante onde a mola está relaxada, temos que a energia do sistema é

E B = U B + K B

Onde

U B = m g x

K B = m v B 2 2

Logo

E B = m g x + m v B 2 2     2 .

Em C a energia do sistema é

E C = E e l , C + K C

Onde

E e l , C = k x 2 2

K C = m v C 2 2

Logo

E C = k x 2 2 + m v C 2 2   .     ( 3 )

Em D a energia do sistema é

E D = E e l , D + U D

Onde

E e l , D = k ( x + A ) 2 2

U D = - m g A

Logo

E D = k ( x + A ) 2 2 - m g A   .     ( 4 )

Passo 4

Igualando as equações (1) e (4), temos

m g L 0 + x = k ( x + A ) 2 2 - m g A  

Como já conhecemos os valores de x , A , k , m e g , vamos substituí-los e isolar L 0

m g L 0 + 3,97 = k ( 3,97 + 11 ) 2 2 - 11 m g

Isolando L 0 temos

L 0 = 185 2 × 75 × 9,80 14,97 2 - 11 - 3,97 = 13,23   m

Como queremos a altura em relação ao ponto mais baixo da trajetória, precisamos somar as alturas

h = L 0 + x + A = 13,23 + 3,97 + 11 = 28,2   m   .

Passo 5

Para responder o item (b) precisamos usar que a amplitude decresce exponencialmente. Assim podemos escrever que

A t = A e - b t 2 m

Como queremos saber o tempo que demora para atingir uma amplitude de 2   m , vamos substituir os valores

2 = 11 × e - 6 t 2 × 75

2 11 = e - 6 t 2 × 75 .

Para isolar o tempo, precisamos aplicar o logaritmo dos dois lados

- 6 150   t = l n 2 11

t = - 150 6 l n 2 11 = 42,6   s     .

Resposta

a )     k = 185   N / m    

b )   v m a x = 17,3   m / s

c )   h = 28,2   m  

d )   t = 42,6   s    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de 500g desliza sobre uma superfície sem atrito com uma velocidade de 0,35m / s . Ele desliza em direção a uma mola de massa desprezível e com constante elástica de 50N / m , a qual se projet
13.1E Uma partícula anda com velocidade de módulo 5,0m/s em um círculo situado no plano x y , cujo raio vale 1,0m . Considere o sistema de coordenadas x y com origem no centro do círculo. No instante
13.3E Um oscilador harmônico apresenta no instante t = 0 os seguintes valores para suas variáveis de movimento: x = - 2,50cm ,v = - 43,3cm/s ,a = 250cm/s² ². Calcule, a amplitude, a frequência angular
Um pequeno bloco é preso a uma mola ideal e move-se em MHS sobre uma superfície horizontal sem atrito. A amplitude do movimento é de 0,165 m. A velocidade máxima do bloco é 3,90 m/s. Qual é o módulo m