Exercícios de Velocidade e Aceleração do MHS - Lista de Exercícios Resolvida
Questão 1
Qual é a constante da fase do oscilador harmônico cuja função aceleração aparece na Fig. 15-56 se a função posição é da forma e ?
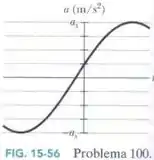
Questão 2
A figura abaixo mostra a posição de um bloco oscilando em MHS na extremidade de uma mola . Quais são
a) a velocidade e b) o módulo da aceleração radial de uma partícula circular uniforme correspondente?
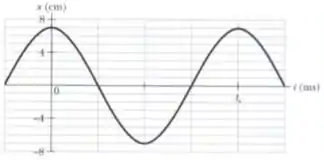
Questão 3
Durante um conserto de uma roda-gigante com raio de metros, um técnico deixa apenas um dos carrinhos instalado. Para testes, a roda é acionada por volta de meio-dia, até atingir uma velocidade angular constante correspondente a uma volta a cada segundos, no sentido anti-horário. O técnico então observou que a sombra do carrinho projetada no chão descreve um movimento harmônico simples. Suponha que o técnico começou a observar a sombra quando o carrinho se encontrava no alto da trajetória. (Adote o ponto central da projeção como origem do eixo e considere que a sombra possui velocidade inicial negativa).
- Encontre a amplitude do movimento da sombra projetada no solo.
- Encontre o período e a frequência angular deste movimento.
- Escreva as equações que descrevem a posição, a velocidade e a aceleração da sombra em função do tempo neste movimento harmônico simples.
- Faça um gráfico da sombra em função do tempo para dois períodos. No gráfico devem estar indicados, numericamente, os valores máximo e mínimo da posição e os tempos em que a sombra atinge esses pontos.
Questão 4
. Abaixo temos o gráfico da aceleração de um oscilador harmônico simples em função do tempo. A expressão que determina a posição, em metros, desse oscilador em função do tempo é
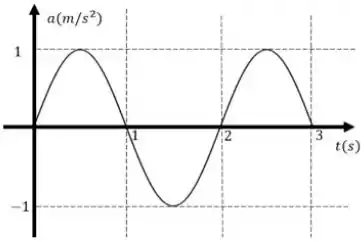
Questão 5
Considere o gráfico abaixo, que representa a posição de um oscilador harmônico simples.
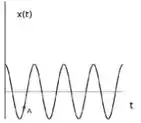
Quando o sistema encontra-se no ponto , podemos afirmar que:
Escolha uma opção:
A posição e a velocidade são ambas negativas e a aceleração é positiva.
A posição e a velocidade são ambas positivas e a aceleração é positiva.
A posição é positiva, a velocidade é negativa e a aceleração é nula, pois é um ponto de inflexão da curva.
A posição é positiva, a velocidade é nula e a aceleração é negativa.
A posição é negativa e a velocidade e a aceleração são positivas.
Ver solução completaQuestão 6
Um objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
b) A velocidade máxima do objeto é:
Ver solução completaQuestão 7
Um objeto de massa m oscila em um movimento harmônico simples. Sabendo-se que a distância máxima em relação ao ponto de equilíbrio é dada por A, que o período é T e que no instante t=0 o objeto está na origem, x=0, mas movendo-se na direção –x, mostre que (Obs: Estas equações são válidas para qualquer Oscilador Harmônico Simples):
c) A aceleração máxima do objeto é dada por:
Ver solução completaQuestão 8
Uma partícula de executa um MHS com uma amplitude de , uma aceleração máxima de módulo e uma constante de fase desconhecida . Determine o período do movimento a velocidade máxima da partícula e a energia mecânica total do oscilador. Qual é o módulo da força que age sobre a partícula no ponto no qual o deslocamento é máximo? O deslocamento é metade do deslocamento máximo?
Ver solução completaQuestão 9
Uma mola, de massa desprezível, está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição tal que a mola se encontra no estado relaxado. Em seguida, o objeto é liberado e passa a oscilar para cima e para baixo, com a posição mais baixa abaixo de . Qual a frequência das oscilações? Qual é a velocidade do objeto quando se encontra abaixo da posição inicial? Um objeto de massa é preso ao primeiro objeto, após o que o sistema passa a oscilar com metade da frequência original. Qual é a massa do primeiro objeto? A que distância abaixo de está a nova posição de equilíbrio (repouso), com dois objetos presos à mola?
Ver solução completaQuestão 10
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
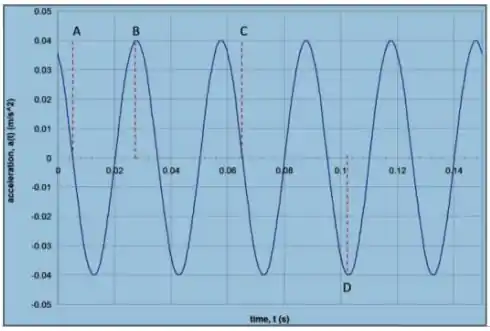
A velocidade máxima do corpo.
Ver solução completaQuestão 11
Na figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
b. A frequência angular do movimento.
Ver solução completaQuestão 12
. Um bloco está pendurado em uma mola, em repouso na posição de equilíbrio. Nesta situação a deformação da mola vale . O bloco é então puxado para baixo, alongando a mola, de mais , e abandonado a partir do repouso. Se necessário, use e deixe as respostas em termos de .
Determine a frequência angular e o período das oscilações subsequentes.
Determine a amplitude e a constante de fase da função que descreve o movimento do bloco. Escolha um eixo de coordenadas orientado verticalmente para cima, com origem no ponto onde o bloco está inicialmente em equilíbrio.
Determine a velocidade máxima alcançada pelo bloco.
Determine o instante em que pela primeira vez a energia cinética se iguala à energia potencial.
Ver solução completaQuestão 13
Na figura ao lado está representado um sistema oscilatório que consiste de um disco de massa M que pode rolar enquanto preso a uma mola de constante elástica k. A mola tem uma de suas extremidades presa à uma parede. O disco é puxado de uma distância A e então solto. Usando apenas essas três grandezas, determine:
a. A velocidade do disco ao passar pela posição de equilíbrio.
Ver solução completa