No seu laboratório de física, você e seu parceiro se laboratório empurram um bloco de madeira com uma massa de (partindo do repouso), com uma força horizontal constante de ao longo de um chão de madeira. Na reunião de laboratório da semana anterior, o seu grupo havia determinado que o coeficiente de atrito cinético não era exatamente constnate, mas que variava com a rapidez do objeto de acordo com a expressão . Em uma planilha, escreva um programa que use o método de Euler para calcular e fazer o gráfico da rapidez e da posição do bloco como uma função do tempo de a . Comparar esse resultado com o que você encontraria supondo que o coeficiente de atrito cinético tivesse um valor constante de .
Passo 1
Começamos explicando a ideia do método de Euler. Vamos escolher um intervalo de tempo pequeno, do tipo , e então fazer a conta em passos.
Nós começamos com rapidez zero, posição zero e tempo zero. A aceleração segue uma fórmula:
Onde segue a fórmula que foi dada no enunciado, começando com e consequentemente:
Vamos ilustrar os primeiros passos, e então fazemos o restante usando a planilha:
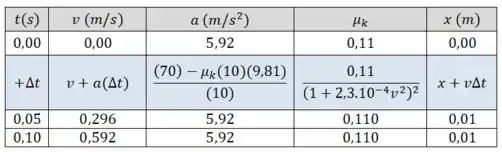
Para chegar até , conforme o enunciado pediu, vamos precisar de um total de passos.
Passo 2
Vamos jogar isso no programa de planilhas, repetir pelo número de vezes necessário, e então fazer um gráfico da posição em função do tempo:

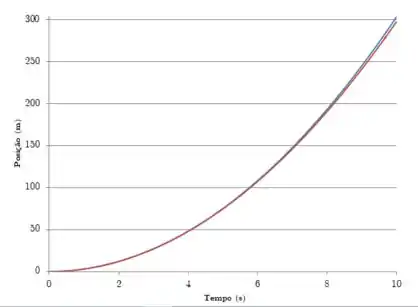
E para comparar isso com o caso em que o coeficiente de atrito é constante só precisamos fazer uma pequana alteração na nossa planilha.
Exclua a coluna que calcula o coeficiente de atrito, e simplesmente mantenha a aceleração sempre igual ao valor inicial. Nesse caso, ficamos com o seguinte gráfico (representado em vermelho ao lado da original):
Passo 3
Agora, usando os mesmos dados, fazemos os gráficos da rapidez em função do tempo:
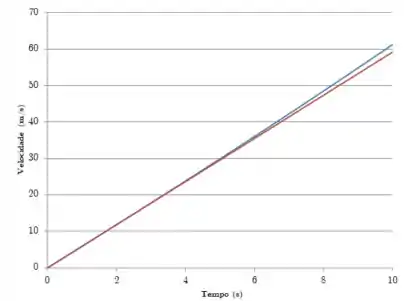
Assim como antes, o gráfico azul se refere ao coeficiente de atrito variável, e o vermelho representa o coeficiente de atrito constante.
Resposta
Ver gráficos.