Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 35
Um caixote de 100 kg está sobre um tapete felpudo. Um trabalhador cansado empurra o caixote com uma força horizontal de 500 N. Os coeficientes de atrito estático e cinético entre o caixote e o tapete são 0,600 e 0,400, respectivamente. Encontre a magnitude da força de atrito exercida pelo tapete sobre o caixote.
Passo 1
Olá, querido! Ele quer saber a força de atrito sobre o caixote.
A gente tem dois jeitos de calcular a força de atrito: usando atrito cinético ou estático. Qual jeito a gente usa para esse caso?
Decidimos assim: se a força aplicada for maior do que atrito estático máximo , significa que o bloco começou a se mover, então a gente usa atrito cinético ().
Se a força aplicada for menor que o atrito estático máximo, o caixote está parado, e a força de atrito atuando é igual à força aplicada, pois deve haver o equilíbrio de forças na direção horizontal.
Então vamos calcular a força de atrito estático máximo.
Passo 2
Para calcular a força de atrito máxima a gente precisa da força normal sobre o objeto. Vamos fazer um diagrama de corpo livre para nos ajudar a achar essa bonita:
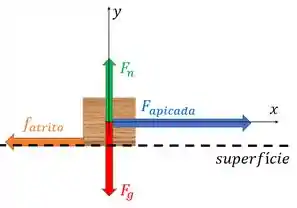
A força peso está sempre para baixo e é sempre perpendicular a superfície.
está na direção . Então para achar , a gente pode aplicar a segunda lei de Newton nessa direção:
Só que o caixote não sobe nem desce, então .
O somatório de forças na vertical é porque a força peso está no sentido negativo de , assim substituindo isso na lei:
Como :
Passo 3
Até aqui, tudo beleza? Agora vamos calcular a força de atrito estático máximo para valer. Ela tem essa fórmulinha:
Onde é o coeficiente de atrito estático que o enunciado diz ser . Substituindo a expressão de na nossa fórmulinha:
Vamos substituir os valores:
Passo 4
Agora vamos comparar a força de atrito estático máximo com a força aplicada. A força aplicada é , menor do que a força de atrito estático máximo, que é de . Então o caixote está parado. Por isso, temos que .
Usando a segunda lei de Newton:
E isso é exatamente o que a gente disse no passo 1, se a força aplicada é menor do que a força de atrito máxima, então a força de atrito atuante é igual a força aplicada.