Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 2.Problemas - Ex. 84
Em seu laboratório de física, você solta um pequeno planador a partir do repouso em diversos pontos em uma rota aérea longa, sem atrito, que está inclinada em um ângulo u acima da horizontal. Com uma fotocélula eletrônica você mede o tempo t necessário para o planador deslizar por uma distância x a partir do ponto de lançamento até o final da rota. Suas medições são dadas na Figura P2.84, que mostra um polinômio de segundo grau (quadrático) ajustado aos dados plotados.
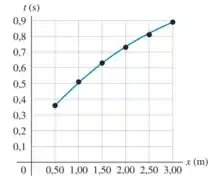
Você deverá encontrar a aceleração do planador, que é considerada constante. Há algum erro em cada medição, de modo que, em vez de usar um único conjunto de valores x e t, você pode ser mais preciso se usar métodos gráficos para obter seu valor medido da aceleração a partir do gráfico. (a) Como você pode refazer o gráfico dos dados de modo que os pontos de dados fiquem mais próximos de uma linha reta? (Dica: você poderia desenhar x, t ou ambos, elevado a alguma potência.) (b) Construa o gráfico descrito na parte (a) e ache a equação para a linha reta que melhor se encaixe aos pontos de dados. (c) Use a linha reta da parte (b) para calcular a aceleração do planador. (d) O planador é lançado a uma distância x 1,35 do final da rota. Use o valor da aceleração obtido na parte (c) para calcular a velocidade do planador quando ele alcança o final da rota.
Passo 1
Eaeee, belezinha??? Bom... o enunciado nos dá o seguinte gráfico:
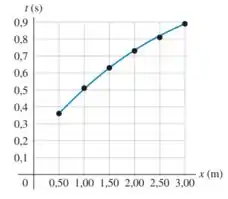
Queremos refazer o gráfico dos dados de modo que os pontos de dados fiquem mais próximos de uma linha reta.
Com o novo gráfico, devemos calcular a aceleração do planador.
Bom... Vamos interpretar os dados em um gráfico para tirar conclusões sobre o movimento de um planador com aceleração constante que segue uma pista de ar sem atrito, partindo do repouso no topo.
As fórmulas cinemáticas de aceleração constante se aplicam.
Vamos pegar o eixo ao longo da superfície do trilho apontando para baixo.
Passo 2
Letra a:
Para aceleração constante começando do repouso, temos .
Onde é o espaço percorrido, é a aceleração e é o tempo.
Portanto, um gráfico de x versus deve ser uma linha reta e a inclinação dessa linha deve ser .
Passo 3
Letra b:
Para construir o gráfico de x versus , podemos usar leituras do gráfico dado no texto para construir uma tabela de valores para x e . O resultado é um gráfico semelhante ao mostrado na figura abaixo:
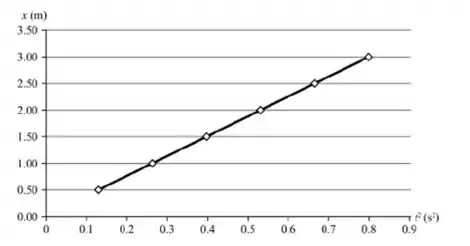
O gráfico tem claramente uma linha reta com inclinação e a interceptação x em . A equação desta reta é , onde x está em metros e t em segundos.
Passo 4
Letra c:
A inclinação da linha reta no gráfico é
Passo 5
Letra d:
Sabemos que a distância percorrida é , a aceleração é , e a velocidade inicial é zero, então usamos a equação e resolvemos para , chegando em .
Lembrando que é a velocidade final, é a velocidade inicial, é o espaço final e é o espaço inicial.
Resposta
- Um gráfico de x versus deve ser uma linha reta e a inclinação dessa linha deve ser .
- Olhar gráfico