Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 83

83. A nave interestelar Enterprise retorna de uma “dobra espacial” para o espaço ordinário com uma velocidade de 50   k m / s . Para grande surpresa da tripulação, uma nave Klingon encontra-se 100   k m diretamente à frente, deslocando-se na mesma direção e sentido a

meros 20   k m / s . Se não realizar manobras evasivas, a Enterprise seguirá em frente e colidirá com os Klingons exatamente em 3,0   s . Os computadores da Enterprise reagem instantaneamente a fim de parar a nave. Que módulo de aceleração a Enterprise necessita

desenvolver a fim de evitar, “por pouco”, uma colisão com a nave Klingon? Considere que a aceleração seja constante. Dica: Trace um gráfico da posição versus tempo que represente os

movimentos tanto da Enterprise quanto da nave Klingon. Escolha x 0 = 0   k m como a localização de onde a E n t e r p r i s e sai da dobra espacial. Como você ilustra graficamente a situação em que a colisão deve ser evitada “por pouco”? Uma vez que você tenha decidido como isto é revelado graficamente, expresse essa situação de forma matemática.

Passo 1

Primeiro, antes das contas vamos ver como fica o gráfico da dica do enunciado pois isso pode nos ajudar a entender o problema.

A nave Klingon está se movendo com velocidade constante, logo, seu gráfico de posição versus tempo é uma reta onde a posição inicial é x K 0 = 100   k m . A Enterprise teremos uma desaceleração, logo seu gráfico é uma parábola virada para baixo.

Quando o enunciado se refere a situação de por pouco uma nave encontra na outra a Enterprise não precisa parar, mas apenas diminuir sua velocidade rápido o suficiente para ter a mesma velocidade da Klingon no ponto em que ela alcança a Klingon.

Então nos gráficos das naves, teremos um momento em o gráfico da Enterprise será tangente ao gráfico da Klingon, isso significa que as duas naves têm a mesma velocidade na mesma

posição.

Levando para a matemática temos que no tempo t 1 as duas naves terão a mesma posição ( x E 1 = x K 1 ) e a mesma velocidade ( v E 1 = v K 1 ) .

E queremos saber a aceração que faz isso ser possível.

Assim a equação que que dá o gráfico da Klingon é:

x K 1 = x K 0 + v K 0 t

E a que dá o gráfico das Enterprise é:

x E 1 = v E 0 t 1 + 1 2 a t 2

Do enunciado conseguimos tirar a seguintes informações:

x E 0 = 0                     v E 0 = 5 0   k m / s

t 0 = 0                     x K 0 = 100   k m

a K = 0                   v K 0 = 20   k m / s

v K 1 = v K 0                     x E 1 = x K 1

v E 1 = v K 1

Passo 2

Agora através daquelas equações podemos montar os seguintes gráficos:

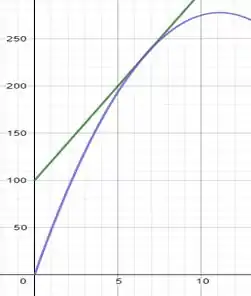
O ponto onde os gráficos se encostam é o instante t 1 que é quando as naves têm a mesma velocidade na mesma posição.

Passo 3

Agora vamos partir para matemática. Temos o seguinte:

x K 1 = x K 0 + v K 0 t

x E 1 = v E 0 t + 1 2 a t 2

E como discutimos para t = t 1 temos:

x K 1 = x E 1

Assim:

x K 0 + v K 0 t 1 = v E 0 t 1 + 1 2 a t 1 2

Passo 4

Agora vamos analisar o seguinte, temos que:

v E 1 = v E 0 + a t

E para t = t 1 , temos que:

v K 1 = v K 0 = v E 1

Assim temos que:

v K 0 = v E 0 + a t 1

Isolando t 1 temos:

t 1 = ( v K 0 - v E 0 ) a

Passo 5

Agora usando a expressão que chegamos no passo 3 e substituindo o que encontramos no passo anterior temos:

x K 0 + v K 0 ( v K 0 - v E 0 ) a = v E 0 ( v K 0 - v E 0 ) a + 1 2 a ( v K 0 - v E 0 ) a 2

⇒ x K 0 = - v K 0 - v E 0 v K 0 - v E 0 a + v K 0 - v E 0 2 2 a

⇒ x K 0 = - v K 0 - v E 0 2 a + v K 0 - v E 0 2 2 a

Assim temos que:

x K 0 = - v K 0 - v E 0 2 2 a

Agora vamos isolar a que é o que queremos saber, assim:

a = - v K 0 - v E 0 2 2 x K 0

Substituindo o que sabemos, temos:

a = - 20 - 50 2 2 ( 100 )

= - 900 200

Assim temos que:

a = - 4,5   k m / s 2

Resposta

a = - 4,5   k m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A Fig. 2-41 mostra a aceleração a em função do tempo t para uma partícula que se move ao longo do eixo x . A escala vertical do gráfico é definida por a s = 12,0m / s 2 . No instante t=- 2,0s , a velo
Um trem partiu do repouso com aceleração constante. Em um certo instante, estava se movendo a 30m / s ; 160m adiante, estava se movendo a 50m / s calcule:(a) a aceleração, (b) o tempo necessário para
Deixa-se cair uma pedra, sem velocidade inicial, do alto de um edifício de 60m . A que distância do solo está a pedra 1,2s antes de chegar ao solo?
Uma partícula parte da origem em t = 0 e se move no sentido positivo do eixo x . O gráfico da velocidade da partícula em função do tempo é mostrado na Fig. 2-43; a escala vertical é definida por v s =