Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 49
Um foguete meteorológico de é carregado com de combustível e disparado diretamente para cima. Ele acelera para cima a por , quando então acaba o combustível. Desconsidere os efeitos da resistência do ar.
- Qual é a máxima altitude alcançada pelo foguete?
- Quanto tempo ele permanece no ar antes de se chocar com o solo?
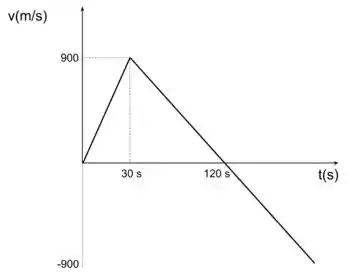
- Trace um gráfico da velocidade versus tempo para o foguete desde a decolagem até bater no solo.
Passo 1
Se liga! O exercício nos fornece informações sobre a massa, mas não precisaremos usá-las.
No item (a) precisamos levar em consideração que o foguete é acelerado. Enquanto ele é acelerado a altura que ele chega é
Considerando que ele parte do repouso, temos
Passo 2
Depois que o combustível acaba, o objeto passa a se deslocar com uma desaceleração de . A velocidade neste instante é
A altura que ele sobe após o combustível acabar pode ser calculada via equação de Torricelli.
Considerando que na altura máxima a velocidade é igual a ZERO, temos
A altura máxima é
Passo 3
Para saber o tempo que o foguete permanece no ar, separaremos o tempo em 3 partes. A primeira parte é quando o foguete sobe acelerado.
é o tempo que o objeto sobe depois que acaba o combustível. Para achar esse valor podemos usar o tempo de subida num lançamento vertical, onde a velocidade de lançamento é .
O tempo é o tempo de queda. Podemos usar o tempo de um objeto caindo em queda livre de uma altura de .
O tempo total é
Passo 4
No item (c) só precisamos montar o gráfico.
