Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 68
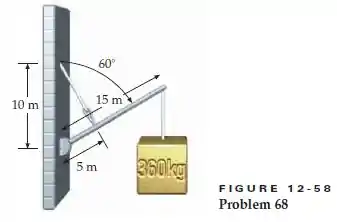
Um corpo de 360 kg é suspenso por um arame preso a uma barra de aço de 15 m, que está articulada em uma parede vertical e suportada por um cabo, como mostrado na Figura 12-58. A massa da barra é 85 kg. Com o cabo preso à barra a 5,0 m da extremidade mais baixa, como mostrado, quais são a tração no cabo e a força exercida pela parede sobre a barra de aço?
Passo 1
Então galera, o que está acontecendo aqui? Nós temos uma barra de aço está sendo mantida fixa na pare com auxílio de um cabo. Esta barra esta sustentando um corpo de massa m.
Podemos concluir que esta barra está em equilíbrio, ou seja, as duas condições do equilíbrio são satisfeitas:
Agora vamos desenhar esta situação, colocando as forças que atuam sobre esta escada:
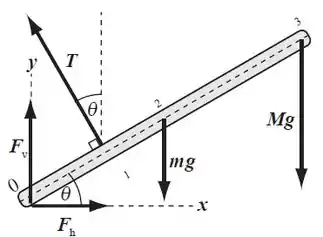
No centro de gravidade, ou seja, no ponto central da barra de aço, temos a força gravitacional sendo aplicada para baixo. Dada por:
Também temos a força peso atuando sobre o corpo que está pendurado:
Como nós temos duas superfícies em contato, existe a força normal , formando um ângulo com o eixo x. Na nossa figura já representamos a força normal decomposta, (eixo y) e (eixo x).
Como temos um cabo suportando a barra, temos uma força de tração (T) no cabo, formando 90° com a barra.
Passo 2
Bom, temos que começar optando por usar uma das condições do equilíbrio, neste caso eu vou usar .
O torque é calculado como:
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher o ponto onde a barra entra em contato com a parede como nosso eixo.
Beleza ! Quando fazemos isso a força normal está no ponto a força de tração está na posição , força da gravidade, e a força sobre o corpo,
Uma observação muito importante ! Para que haja torque, devemos achar as componentes da força que forma 90° com a barra. Para a tração não vamos precisar achar as componentes porque ela já possui este ângulo.
Então, vamos começar com as forças peso que estarão opostas ao ângulo:
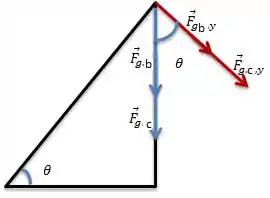
Então,
Já temos r e as forças perpendiculares, agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. As forças peso são capazes de girar a barra no sentido horário (-), já a tração gira no sentido anti-horário (+).
Jogando toda informação na segunda condição:
Isolando T:
Nós temos todos os dados que precisamos:
Pela figura:
Na fórmula da tração:
Muito bom! Um já foi, agora queremos saber força exercida pela parede sobre a barra de aço.
Passo 3
Para a força normal exercida pela parede, nós vamos ter um triângulo retângulo formado:
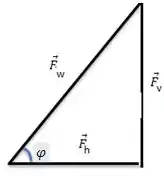
Então, a força exercida pela parede será a hipotenusa de um triângulo retângulo:
Para caracterizar este vetor nós precisamos do ângulo formado entre esta força e a horizontal. Podemos calcular o ângulo como:
Já sabemos calcular, mas o problema é que não temos nenhuma das forças. Então precisamos achar as forças. E como fazer isto?
Podemos usar a primeira equação do equilíbrio. Se , então .
Muito bem, agora vamos separar as forças. Na direção x nós temos a força normal () e a tração na direção x (), com sentidos opostos:
Na direção y, temos as forças da gravidade, para baixo, e a força normal () e a tração na direção y (), voltadas para cima:
Substituindo na equação da força normal:
Já temos todos os valores:
Agora só precisamos achar a direção:
Ou seja, 41,5° abaixo do eixo x.