Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 56
Uma lata de tinta spray, selada e praticamente vazia, ainda contém uma quantidade residual do propelente: 0,020 mol de gás nitrogênio. A etiqueta na lata alerta claramente: “Não incinerar”.
- Explique este alerta e desenhe um diagrama PV para o gás no caso de a lata ser submetida a uma temperatura alta;
- Você está encarregado de testar a lata. O fabricante alega que ela pode suportar uma pressão interna de gás de 6 atm antes de explodir. A lata está, inicialmente, nas condições normais de temperatura e pressão em seu laboratório. Você inicia o aquecimento da lata uniformemente, usando um aquecedor com uma potência de saída de 200W. A lata e o aquecedor estão em um forno isolado e você pode supor que 1% do calor liberado pelo aquecedor seja absorvido pelo gás na lata. Quanto tempo você espera que o aquecedor permaneça acesso antes de a lata explodir?
Passo 1
Legal, vamos começar desenhando o diagrama PV na letra a. O volume é fixo, ou seja o volume da lata não varia quando a temperatura aumenta. Podemos concluir algo dessa afirmação, certo?
Se não há variação do volume, não há trabalho! É fácil perceber que se não existe trabalho, quando o calor é fornecido para lata as moléculas dos gases se agitarão, aumentando sua energia interna e, consequentemente, a pressão do sistema.
No diagrama:
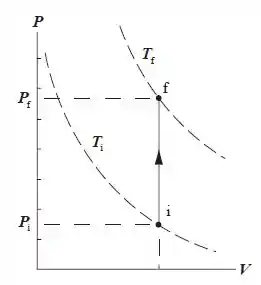
Por que isso é perigoso? Se o volume é constante, a pressão aumenta até o máximo possível , até que a estrutura da lata não suporta a pressão e explode, gerando uma grande explosão de estilhaços.
Menos uma ! Que venha a letra b!
Passo 2
Bom, na letra b queremos saber quanto tempo o aquecedor deve permanecer aquecendo a lata antes dela explodir. Para relacionar o tempo e o calor fornecido pelo aquecedor podemos usar a equação da potencia:
Isolando
A pressão nós já temos. Agora precisamos de quanto calor deve ser fornecido pelo aquecedor.
Vamos guardar essa informação por enquanto e trabalhar no calor que deverá ser adicionado à lata. Como não há trabalho, a primeira lei da termodinâmica nos diz que:
A energia cinética é dada por:
Onde g é referente aos graus de liberdade. Para uma molécula diatômica, como o,
Substituímos na equação do tempo:
Chegamos na equação do tempo, mas ainda não conseguimos resolver porque não temos a variação da temperatura.
Para sair desse empasse precisamos de usar alguns artifícios matemáticos. Se lembrarmos da equação dos gases:
Sabemos que nR é constante, para o estado inicial e final, então:
Como o volume é constante:
Então:
No enunciado do problema temos que:
Substituindo na equação anterior:
Se sabemos disso, conseguimos calcular
Jogando na equação do tempo:
Passo 3
Agora sim ! Achamos uma equação do tempo em função de variáveis que conhecemos.
Para a potência temos que prestar atenção no fato que apenas 1% do calor do aquecedor é absorvido, sendo assim:
Substituindo tudo na formula do passo 2:
Transformando em minutos:
E finalizamos a questão !