Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 12.5 - Ex. 9
Um lavador de janelas de 75Kg usa uma escada com 10Kg de massa e 5,0m de comprimento. Ele apoia uma extremidade no chão a 2.5m de uma parede, encosta a extremidade oposta em uma janela rachada e começa a subir. Quando percorreu uma distancia de 3,0m ao longo da escada, a janela quebra. Despreze o atrito entre a escada e a janela e suponha que a base da escada não escorregue. Quando a janela está na iminência de quebrar, qual é
a) o modulo da força que a escada exerce sobre a janela;b)o modulo da força que o chão exerce sobre a escada;c) o angulo (em relação à horizontal) da força que o chão exerce sobre a escada?
Passo 1
(a)Como em todas as questões que envolvem equilíbrio, vamos primeiro analisar as forças que atuam sobre a escada:
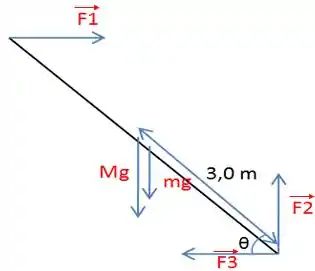
Nesse caso:
é a força que a janela exerce sobre a escada;
é a massa do lavador;
é a massa da escada;
é a componente horizontal de reação do piso;
é a componente vertical de reação do piso;
é o ângulo que a escada forma com o piso.
Além disso, vamos chamar de o comprimento que o lavador percorreu ao longo da escada , que é igual a .
Passo 2
Como a escada está em equilíbrio, a soma dos torques com relação ao pé da escada em contato com o piso é nulo. Como e estão sobre o eixo de rotação (pé da escada), elas não exercem torque. Assim, temos:
Onde:
Repara que pegamos apenas as componentes perpendiculares entre as forças e as distâncias! Já que o torque é definido por:
Passo 3
Isolando na equação de cima, temos:
Como a força que a escada exerce na janela é, em módulo, igual à força que a janela exerce sobre a escada, a resposta dessa letra é:
Passo 4
(b)Agora, vamos analisar o equilíbrio de forças na horizontal e na vertical.
Na horizontal, temos:
Como já calculamos o valor de antes, temos que
Na vertical:
Então:
Para saber o módulo da força que o chão exerce sobre a escada, vamos considerar o módulo da força resultante de e :
Passo 5
(c)Para encontrarmos o valor de , basta usarmos o fato de que esse ângulo é igual ao formado entre a horizontal e a resultante das forças e . Assim, temos que:
O ângulo menor que graus que possui essa tangente é aproximadamente .
Resposta
(a)
(b)
(c)