Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 40
Uma bola de esta suspensa por um fio de aço de de comprimento e de raio. Qual é a elongação do fio?
Passo 1
Ola! Ele quer a enlongação do fio. Ou seja, ele quer saber a variação de comprimento do fio quando ele é puxado. E por que esse fio é puxado? Vamos fazer esquema da situação:
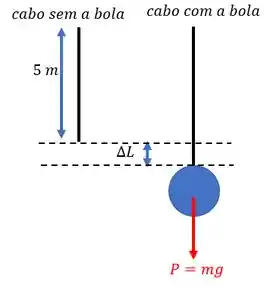
O peso da bola vai causar uma tensão no cabo. Essa tensão é a força que tende a esticar o cabo, gerando um enlongamento em relação ao comprimento original do cabo.
Para achar esse elongamento, vamos usar a fórmula do módulo de Young:
Nela é o nosso enlongamento, é a tensão no cabo, é o comprimento inicial do cabo e a área da seção transversal do cabo. E é o módulo de Young, que é tabelado para cada material.
A ideia é a gente usar essa fórmulinha para achar o que o enunciado pede. Mas não se esqueça de passar todas as distâncias para metros e usar o módulo de Young em Vamos!
Passo 2
Como queremos achar a elongação, isto é, de quanto se esticou o fio, vamos isolar o termo . Usando a propriedade de divisão de frações
Como ele nos deu o raio do fio, vamos considerar que o cabo tem seção transversal circular. Logo sua área é dada por
Com
Como temos uma bola suspensa e não temos forças externas, a nossa tensão no cabo será o próprio peso dessa bola que puxa ele para baixo, isto é,
O valor do modulo de Young para o aço é o seguinte:
Ele é um valor tabelado. No livro, você pode encontra-lo na tabela 12.1. Substituindo esses dados e expressões na fórmulinha, temos
Passo 3
Agora vamos substituir os valores na nossa expressão e correr pro abraço.
Fazendo as contas: