Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 83
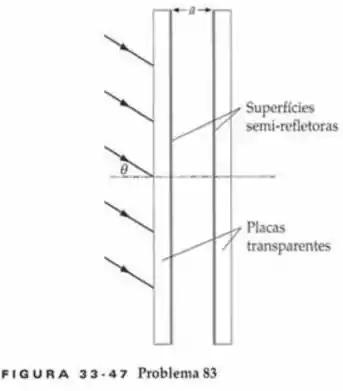
Um interferômetro Fabry-Perot (Figura 33-47) consiste em dois espelhos paralelos, semitransparentes que estão de frente um para o outro, separados por uma pequena distância a. Um espelho semitransparente é tal que transmite 50 por centro e reflete 50 por cento da intensidade incidente. Mostre que, quando luz incide no interferômetro em um ângulo de incidência , a luz transmitida terá um máximo de intensidade quando .
Passo 1
Meus lindos e minhas lindas!
O interferômetro de Fabry-Perot está representado na figura abaixo. Para uma interferência construtiva na transmissão de luz, a diferença de trajetória deve ser dada por um múltiplo inteiro do comprimento de onda da luz.
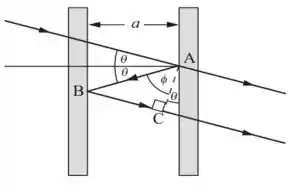
Após análise do diagrama e do enunciado, sabemos que:
E, também, que:
Pela geometria do diagrama, por trigonometria, podemos garantir que:
Seguindo:
Passo 2
Pelas equações encontradas acima, vamos desenvolver a última encontrada:
Pelo diagrama, podemos observar que:
Aplicando:
Amigos e amigas, por trigonometria, quem é ? Isso mesmo que vocês pensaram!
Substituindo:
Sabemos que :
Por trigonometria, há uma identidade que nos garante que:
Vamos aplicar:
Passo 3
Após termos desenvolvido a segunda equação, só nos resta igualar as equações:
Seguindo:
Resposta
Ei, a resposta está no passo a passo :)