Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas Adicionais - Ex. 116
Mostre que a distância entre um objeto e a imagem real formada por uma lente convergente delgada é sempre maior ou igual a quatro vezes a distância focal da lente.
Passo 1
E aí meus caros(as)! A nossa missão agora é solucionar a questão 116!
Bem! E o que a gente tem aqui é uma questãozinha sobre formação de imagens em lentes corvengente!
Para entender o que está acontecendo vamos dar uma olhada na figura abaixo...
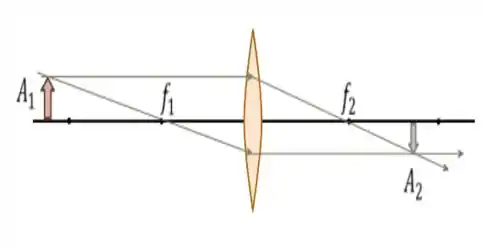
É assim que ocorre a formação de imagens em uma lente convergente!
Agora, vamos dar nomes aos bois! Chamando de a distância do objeto a lente, de a distância da imagem e de a distância focal... A gente tem que essas variáveis vão estar relacionadas pela seguinte equação, típica de lentes delgadas:
E essas três grandezas aí, pela situação descrita no enunciado, são positivas!
onsidere dois raios de luz, r e r, que estão acima e abaixo do raio normal (o raio que refaz
Passo 2
Agora, vamos chamar de a distância do objeto até a imagem... Em lentes convergentes, temos que...
Isolando ...
E substituindo isso na equação do ...
Isolando ...
Obtemos uma equação de em função da distância do objeto e da distância focal !
Passo 3
A gente quer determinar a distância entre um objeto e a imagem real formada por uma lente convergente delgada é sempre maior ou igual a quatro vezes a distância focal da lente. Ou seja, estamos trabalhando com um valor mínimo admissível!
Sendo assim, para determinar o valor mínimo de , derivamos em relação a e igualamos o resultado a zero...
E então, é só substituir esse valor em ...
Pra finalizar! Falta ver se esse valor é um mínimo ou máximo! Pra isso, vamos recorrer ao teste da segunda derivada!
Substituindo ...
Como o valor é positivo, então é um ponto de mínimo! Logo, a distância vai ser a distância mínima que estávamos procurando!
Pronto! Finalizamos aqui! Bora pra próxima!