Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 86

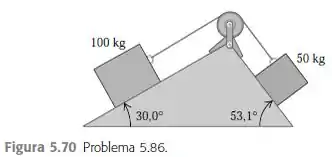
Dois blocos estão conectados por uma corda que passa sobre uma polia fixa sem atrito e repousam sobre planos inclinados (Figura 5.70 ).

a) Como os blocos devem se mover quando forem soltos a partir do repouso?

b) Qual é a aceleração de cada bloco?

c) Qual é a tensão na corda?

Passo 1

Fala galera, tudo bem? Essa questão parece complicada, mas calma! Vou ajudar você aqui!

Temos o seguinte sistema:

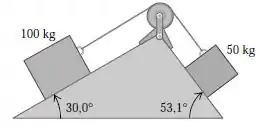
Despreze o atrito aí, viu?

O enunciado nos faz três perguntinhas:

a) Como os blocos devem se mover quando forem soltos a partir do repouso?

b) Qual é a aceleração de cada bloco?

c) Qual é a tensão na corda?

Bom... A ideia pra resolver esse tipo de problema é tipo receita de bolo. Não sou nenhuma Ana Maria Braga, mas essa eu posso compartilhar com você!

Resumindo nós precisamos: desenhar o diagrama do corpo livre, identificar as forças e aplicar a segunda lei. A partir daqui cada exercício segue seu rumo.

Beleza? Então vou começar a resolver esse exercício aqui. Vamos lá?

Passo 2

  1. Em cada bloco nós teremos 4 forças atuando:

    2. - A força peso, para baixo (em vermelho);

    - A força normal, perpendicular ao plano (azul);

    - O atrito, que será paralelo ao plano e contrario ao movimento;

    - Tensão, que conecta os dois blocos (verde).

    Saca só esse diagrama de corpo livre vai ficar:

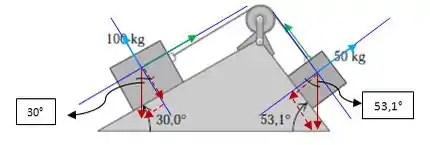
    Se liga numa coisa! A força peso está em vermelho: o vetor contínuo é o vetor “de verdade” e pontilhado estão as componentes.

    A gente ainda não sabe se eles irão se mover, ou seja, se não há uma compensação nas forças e tudo fica em equilíbrio.

    Isso a gente vai saber quando calcular essas componentes: se forem iguais em módulo, os blocos não vão se mover; se forem diferentes o sistema vai adquirir velocidade e assim uma aceleração.

    Com o sistema solto são as componentes horizontais da força peso de cada bloco vão puxar o sistema para cada lado e quem tiver maior módulo vai comandar o movimento de todo mundo.

    A componente horizontal da força peso P é:

    P x = P sen ⁡ θ

    Onde θ = 30 °   para o bloco de 100   kg , e θ = 53,1 ° para o bloco de 50   kg .

    Bora calcular!

    Passo 3

    Então para o bloco de maior massa:

    P 100 = 100 ⋅ 9,8 ⋅ sen ⁡ 30

    P 100 = 490   N

    E para o bloco de menor:

    P 50 = 50 ⋅ 9,8 ⋅ sen ⁡ 53,1

    P 50 = 391,8   N

    Então como P 100 > P 50 , quer dizer que o bloco que manda nesse movimento todo é o de 100   kg . Assim todo sistema vai se mover para a esquerda.

    Passo 4

  2. A aceleração de cada bloco é igual para o sistema todo, pois eles me movem juntos! Sem deslizamento! A aceleração vai ser dada a partir da segunda lei:

    3. P 100 - P 50 = ( 100 + 50 ) a

    a = 490 - 391,8 150

    a = 0,65   m/ s 2

    Tranquilo até aqui?

    Passo 5

  3. Para determinar a tensão precisamos isolar algum dos blocos. Vou escolher o bloco de 100 k g . Nele está agindo a força peso P x para a esquerda e a força tensora T para a direita. A aceleração é aquela que calculamos no passo anterior. Juntando tudo na segunda lei teremos:

P x - T = 100 ⋅ 0,65

T = P x - 65 = 490 - 65

T = 425   N

Resposta

  1. Para esquerda.
  2. 0,65   m/ s 2 , para a esquerda.
  3. T = 425   N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na máquina de Atwood discutida no Exemplo 4.4 e mostrada na Figura Ativa 4.12a, m 1=2,00k g e m 2=7,00k g . Por comparação, as massas da polia e da corda são desprezíveis. A polia gira sem atrito e a
Uma criança inventiva chamada Nick quer pegar uma maçã em uma árvore sem escalá-la. Sentado em uma cadeira conectada a uma corda que passa sobre uma polia sem atrito (Fig. P4.45), Nick puxa a ponta so
Inicialmente, o sistema dos corpos mostrados na Figura P4.51 é mantido sem movimento. A polia e todas as superfícies não têm atrito. Seja a força F → zero e assuma que m 1 pode se mover apenas vertica
Três corpos estão conectados sobre uma mesa, como mostrado na Figura P5.14. O coeficiente de atrito cinético entre o bloco de massa m 2 e a mesa é 0,350 . Os corpos têm massa de m 1=4,00k g , m 2= 1,0
O sistema mostrado na Figura P4.47 (Capítulo 4) tem uma aceleração de módulo 1,50m / s 2 . Suponha que o coeficiente de atrito cinético entre o bloco e o plano inclinado seja o mesmo para ambos os dec