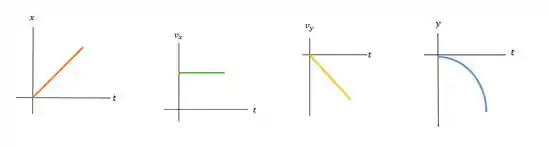
Um livro de física escorrega horizontalmente para fora do topo de uma mesa com velocidade de . Ele colide com o solo em . Desprezando a resistência do ar, ache a) a altura do topo da mesa até o solo; b) a distância horizontal entre a extremidade da mesa e o ponto onde ele colidiu com o solo; c) os componentes da velocidade do livro e o módulo, a direção e o sentido da velocidade imediatamente antes de o livro atingir o solo; d) faça diagramas , , e para o movimento.
Passo 1
Oi, pessoal! Tudo bom? O livro se move em movimento de projétil quando sai do tampo da mesa. Sua velocidade inicial é horizontal e ao longo do tempo ele vai caindo (ou seja, passa a ter uma velocidade vertical).
Vamos tomar a direção como positiva para cima. E tomar como a origem das coordenadas na posição inicial do livro, no ponto em que sai do tampo da mesa.Esboçando a situação:
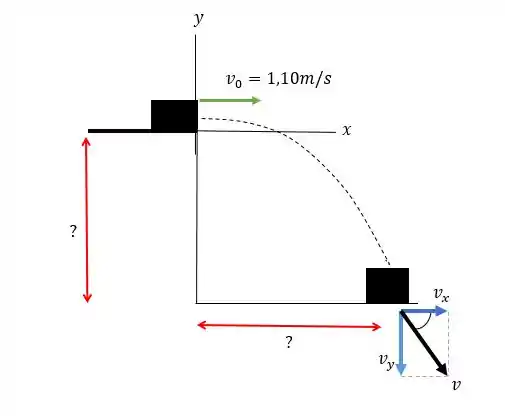
Organizando as informações do enunciado, sabemos que na:
E na:
Agora vamos responder cada item!
Passo 2
(a) Queremos encontrar a altura do topo da mesa , então, vamos utilizar a seguinte equação para o eixo :
Substituindo:
Com isso, tampo da mesa fica a acima do piso.
Passo 3
(b) Agora queremos a distância horizontal entre a extremidade da mesa e o ponto onde ele colidiu com o solo, ou seja, queremos o alcance do livro! Para isso, vamos utilizar a equação da velocidade, mas agora para o eixo (onde temos uma velocidade constante):
Então, a distância que o livro deixa a mesa e cai no chão é de .
Passo 4
(c) Bom, lembrando que a velocidade no eixo x é constante, temos que:
Para encontrarmos a velocidade em , usaremos a mesma equação em relação ao :
Substituindo:
Para encontrarmos o modulo da velocidade primeiro vamos desenhar um esboço das componentes:
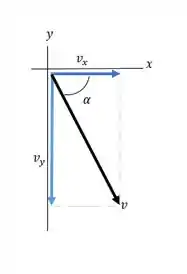
E encontraremos o seu modulo através da equaçãozinha:
Passo 5
Para encontrarmos o ângulo faremos através da seguinte relação:
abaixo da horizontal.
Ou podemos escrever a velocidade final na forma de vetor:
Passo 6
Na direção , e é constante. Na direção , e também negativo, e aumentando em magnitude, já que e estão nas mesmas direções. Os movimentos e ocorrem independentemente, conectado apenas pelo tempo. O tempo que o livro leva para cair é o tempo que ele percorre horizontalmente.
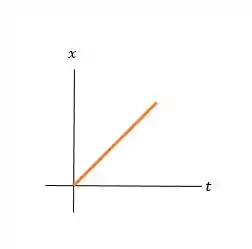
Resposta
- O tampo da mesa fica a acima do piso.
- A distância que o livro deixa a mesa e cai no chão é de .
- e abaixo da horizontal.
d)