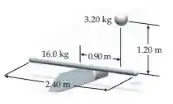
Uma longa barra de , de de extensão, está apoiada, em seu ponto do meio, sobre o fio de uma faca. Uma bola de massa de vidraceiro, de , cai a partir do repouso de uma altura de , sofrendo uma colisão perfeitamente inelástica com a barra a do ponto de apoio (Figura 10-51). Determine a quantidade de movimento angular do sistema barra mais massa em relação ao ponto de apoio, imediatamente após a colisão inelástica.

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos observar que o Torque externo resultante é zero, portanto há conservação da quantidade de movimento angular.

Vamos, então, usar a definição de quantidade de movimento angular e descobrir a velocidade a partir da conservação de energia mecânica.

Por definição, temos:

Usando conservação de energia mecânica, temos:

Como, , temos:

Substituindo na equação da quantidade de movimento angular, temos:

Substituindo os valores, temos: