Exercícios de Conservação do Momento Angular - Lista de Exercícios Resolvida
Questão 1
Um homem com os braços junto ao corpo está em cima de uma cadeira giratória que gira sem atrito. Quando o homem estende os braços:
a) A velocidade angular da cadeira aumenta
b) A velocidade angular da cadeira continua a mesma
c) O momento de inércia do homem diminui
d) A energia cinética do sistema aumenta
e) O momento angular do sistema continua o mesmo
Ver solução completaQuestão 2
Considere as afirmativas abaixo:
(I) Em uma colisão inelástica, o momento linear do sistema nunca é conservado.
(II) A velocidade do centro de massa de um sistema de partículas é sempre constante.
(III) Forças internas nunca alteram o momento linear total de um sistema de partículas.
(IV) O momento linear e o momento angular de um sistema de partículas sempre se conservam sob a ação de um par de forças externas de mesmo módulo, direção e sentidos opostos.
São verdadeiras apenas as afirmativas:
(a) I
(b) III
(c) II e IV
(d) II e III
(e) III e IV
Ver solução completaQuestão 3
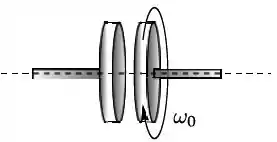
Um disco uniforme é montado em um eixo horizontal de massa desprezível, em torno do qual pode girar livremente, como mostra o diagrama. O momento de inércia do disco em relação ao eixo é . O disco está inicialmente girando com velocidade angular ; vide figura. O disco é movimento horizontalmente para esquerda até que sua face entre em contato com um disco idêntico, que está inicialmente em repouso. Depois de um pequeno intervalo de tempo, os dois discos acoplam-se e passa a girar juntos com uma velocidade angular final . Em relação às grandezas: velocidade angular final, energia cinética de rotação e momento angular do sistema, pode-se afirmar que ao final do processo de acoplamento:
- , não é conservada, não é conservado;
- , é conservada, não é conservado;
- , é conservada, não é conservado;
- , não é conservada, é conservado;
- , é conservada, é conservado;
Questão 4
O rotor de um motor elétrico tem um momento de inércia em relação ao eixo central. O motor é usado para mudar a orientação da sonda espacial no qual está montado. O eixo do motor coincide com o eixo central da sonda; a sonda possui um momento de inércia em relação a esse eixo. Calcule o número de revoluções do rotor necessárias para fazer a sonda girar em torno do eixo central.
Ver solução completaQuestão 5
Uma nave espacial isolada tem um eixo de simetria em relação ao qual seu momento de inércia é . A nave gira em torno desse eixo com velocidade angular constante de módulo . Aciona-se um mecanismo interno da nave que reduz seu tamanho, sem perder sua simetria relativa ao eixo de rotação, de modo que ao final seu momento de inércia relativo a esse eixo se reduz a . A velocidade angular final da nave no tamanho final é dada por
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 6
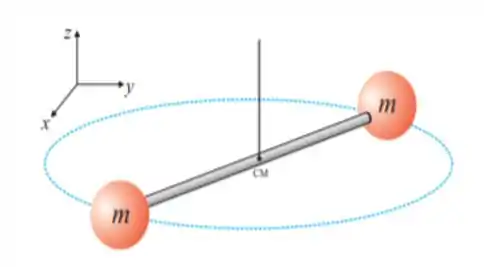
18. O sistema mostrado na figura é formado por duas partículas de massas iguais fixadas às extremidades de uma haste de massa desprezível e com comprimento . O sistema pode girar livremente, sem atrito, em um plano horizontal com velocidade angular em torno de um eixo fixo vertical que passa pelo centro de massa do sistema. Subitamente, um gás comprimido que está no interior da haste a expande até um comprimento de . Diante disso, o módulo do vetor velocidade angular, em radianos por segundo, que o sistema adquire após a expansão é:
Questão 7
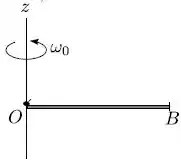
Um caracol de massa encontra-se inicialmente em repouso na extremidade, ponto , de uma barra rígida e homogênea de comprimento (conforme a figura), que gira com velocidade angular em torno de um eixo fixo que passa pelo ponto , perpendicularmente a barra horizontal. Em um certo instante, o caracol desloca-se até a extremidade oposta da barra, ponto , onde permanece. Nesta situação a barra gira com velocidade angular . Sendo , o momento de inércia do sistema com relação ao eixo quando o caracol está no ponto e o momento de inércia do sistema com relação ao eixo quando o caracol está no ponto , das opções abaixo, a correta é
- ;
- ;
- ;
- ;
- ;
Questão 8
Um homem está em pé em uma plataforma que gira (sem atrito) com uma velocidade angular de ; seus braços estão abertos e ele segura um tijolo em cada mão. O momento de inércia do sistema formado por homem, tijolos e a plataforma em relação ao eixo vertical central da plataforma é . Se, ao mover os braços, o homem reduz o momento de inércia do sistema para , determine
a nova velocidade angular da plataforma e
a razão entre a nova energia cinética do sistema e a energia cinética inicial
de onde vem essa energia cinética adicional?
Ver solução completaQuestão 9
Uma nave espacial isolada tem um eixo de simetria em relação ao qual seu momento de inércia é . A nave gira em torno desse eixo com velocidade angular constante de módulo . Aciona-se um mecanismo interno da nave que reduz seu tamanho, sem perder sua simetria relativa ao eixo de rotação, de modo que ao final seu momento de inércia relativo a esse eixo se reduz a . A velocidade angular final da nave no tamanho final é dada por
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 10
Um homem segurando um peso de papel igual em cada mão, com os braços estendidos, está de pé sobre um pedestal que gira sem atrito com velocidade angular de . Nesta posição, o momento de inércia total do sistema (pedestal + homem + pesos) é de .
Quando o homem encolhe os braços, o momento de inércia total muda para . Nesta posição, qual é a velocidade angular do pedestal?
Suponha agora que cada peso de papel tenha uma massa de e que a distância da mão estendida até o eixo do corpo seja de . Se ele largar os pesos e manter os braços estendidos, qual será o novo valor do momento de inércia do sistema (pedestal homem)?
Na situação do item , calcule o novo valor da velocidade angular do sistema após o homem largar os pesos.
Ver solução completaQuestão 11
Uma menina de massa está em pé na borda de um carrossel sem atrito de raio e momento de inércia que está parado. A menina joga uma pedra de massa horizontalmente em uma direção tangente à borda do carrossel. A velocidade da pedra em relação ao chão é . Depois disso, qual é
a velocidade angular do carrossel e
a velocidade linear da garota?
Ver solução completaQuestão 12
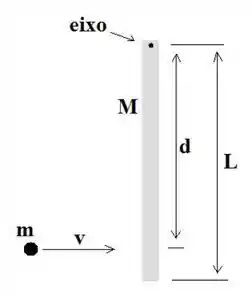
A figura mostra uma barra homogênea pendurada, de comprimento e massa , que gira em torno de um eixo numa de suas pontas. A barra, inicialmente em repouso, é atingida por uma partícula de massa num ponto abaixo do eixo. Admita que a colisão é perfeitamente inelástica. Qual deve ser a velocidade da partícula para que, após a colisão, o ângulo máximo entre a barra e a vertical seja de ?
Utilize .
Questão 13
As rodas e na Fig. 11-61 são conectadas por uma correia que não desliza. O raio de é vezes maior que o de . Qual é a razão entre os momentos de inércia das duas rodas se elas têm (a) o mesmo momento angular em relação aos respectivos eixos centrais e (b) a mesma energia cinética de rotação?

Questão 14
Uma roda de esmeril de possui forma cilíndrica com raio igual a .
c) Calcule o trabalho realizado pelo torque utilizando a definição de trabalho como integral do torque.
Ver solução completaQuestão 15
Uma roda de esmeril de possui forma cilíndrica com raio igual a .
d) Qual é a energia cinética do esmeril quando ele está girando a? Compare sua resposta com o resultado do item c).
Ver solução completaQuestão 16
Um CD de massa e raio está parado e livre para rodar em torno de um eixo que passa pelo seu centro de massa. Na borda do CD um besouro, de massa , começa a se movimentar com uma velocidade que é tangencial à borda. Se o módulo da velocidade do besouro, medida em relação a um ponto fixo na Terra, é de , a velocidade angular do CD vale:
Momento de inércia de um disco cujo eixo de rotação passa pelo seu centro de massa:
Ver solução completaQuestão 17
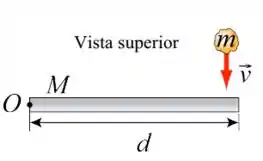
Uma haste fina de massa e comprimento , inicialmente em repouso, pode girar horizontalmente sobre uma mesa, sem atrito, em torno do ponto O, como mostra a figura. Um pedaço de massa de vidraceiro de massa , com velocidade , colide com a haste em uma das extremidades, permanecendo grudado nela.
- Qual é o momento angular do sistema haste+massa imediatamente antes da colisão?
- Qual é a velocidade angular do sistema imediatamente após a colisão?
- Qual é a razão entre a energia cinética do sistema haste+massa depois e antes da colisão?
Dado: O momento de inércia de uma haste de massa M e comprimento d em relação a um eixo que passa pelo seu centro de massa é
Questão 18
Uma barra delgada homogênea de comprimento e massa está inicialmente em repouso como mostra a figura. Preso a uma de suas extremidades há um objeto de massa e dimensões desprezíveis. Um segundo objeto do mesmo tipo move-se na direção do eixo , com velocidade constante. No instante o segundo objeto atinge a outra ponta da barra e adere a ela de forma permanente. Não há atrito no movimento dos objetos sobre o plano horizontal . Use para descrever o movimento da barra o ângulo entre a barra e o eixo , considerando como positivo o sentido anti-horário.
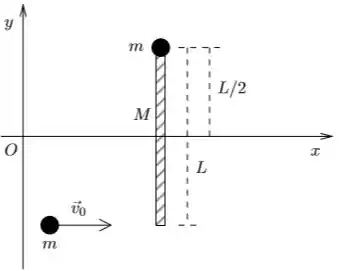
Determine o momento de inércia do conjunto de corpos, depois do choque, em relação a um eixo na direção , passando pelo centro de massa.
Determine a velocidade do centro de massa do conjunto de corpos, depois do choque.
Determine a velocidade angular do conjunto de corpos, depois do choque, em relação a um eixo na direção , passando pelo centro de massa.
Determine a velocidade do segundo corpo, depois do choque, em relação à origem do sistema de coordenadas mostrado na figura.
Ver solução completaQuestão 19
Uma partícula de massa e velocidade desliza sobre uma superfície horizontal e colide com um quadrado formado por barras rígidas de massa desprezível e comprimento , que possui partículas de massa em três dos seus vértices, como mostrado na figura (vista de cima). O quadrado está inicialmente em repouso, e o atrito entre todos os corpos e a superfície pode ser desprezado. Após a colisão, a partícula fica colada ao quadrado no vértice que estava vazio. Expresse todas as respostas em função de , e .
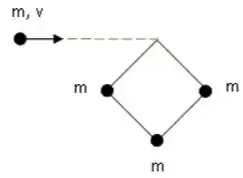
(a) Que grandezas físicas relevantes para o problema são conservadas na colisão? Justifique sua resposta.
(b) Determine o momento de inércia do sistema, após a colisão, em torno do eixo de rotação relevante para o problema.
(c) Determine o vetor velocidade de translação do centro de massa do sistema após a colisão.
(d) Determine o vetor velocidade angular de rotação do sistema em torno do seu eixo.
(e) Qual é a variação de energia cinética do sistema devido à colisão?
Ver solução completaQuestão 20
Um alvo é constituído por uma placa quadrada de lado e massa que pode girar sem atrito em volta de um eixo passando por um dos seus lados. O eixo é fixado horizontalmente numa parede e o alvo colocado na sua posição de repouso, conforme mostrado na figura. Em seguida, ele é atingido frontalmente em seu centro por uma partícula de massa e velocidade que fica retida no centro da placa. Usando o ponto como origem quando for preciso, e supondo ( vezes a massa da partícula), responda às seguintes perguntas, expressando suas respostas em termos de , , e .
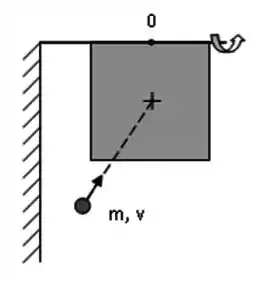
(a) Calcule o momento de inércia total do sistema depois da colisão em torno do seu eixo de rotação, sabendo que o momento de inércia de uma barra delgada de mesma massa e largura em relação a um eixo passando pelo seu centro (e perpendicular à barra) é .
(b) Qual é a velocidade angular da placa logo após o impacto da bala?
(c) Qual é a altura máxima atingida pelo centro de massa da placa antes que ela comece a oscilar em torno da sua posição vertical inferior?
(d) Qual é a aceleração angular da placa, naquela altura máxima, expressada em função do ângulo que ela faz em relação à sua posição de repouso?
Ver solução completaQuestão 21
Um haltere é formado por duas partículas de massa (1 e 2) ligadas por uma haste rígida, de massa desprezível e comprimento . O haltere pode deslizar sem atrito sobre uma mesa. Uma partícula 3 de massa , com velocidade inicial (perpendicular à haste do haltere) colide com uma das partículas, como mostrado na figura.Sendo a colisão perfeitamente elástica, determine

a) Imediatamente após a colisão, a velocidade linear das partículas 2 e 3 (indicando a direção e sentido).
b) O impulso sofrido pela partícula 2.
c) Após a colisão, qual a velocidade linear do centro de massa do haltere?
Ver solução completaQuestão 22
Uma pessoa está com os braços abertos sobre uma plataforma giratória (com atrito desprezível no giro) presa ao chão. Nessa posição, o momento de inércia da pessoa com a plataforma é em relação ao eixo de rotação da plataforma. Um disco uniforme de massa raio é lançado com velocidade e velocidade angular conforme a figura. O disco é agarrado pela mão e para de girar, ficando seu centro a uma distância do centro do sistema pessoa-plataforma, na altura dos braços. Determine:
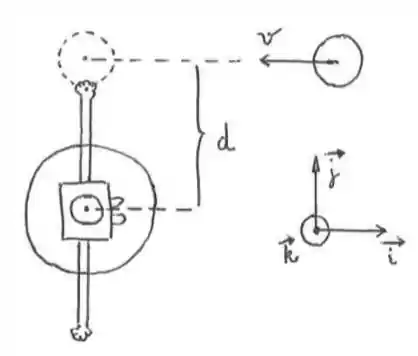
a) O vetor momento angular do disco em relação ao seu centro de massa antes de ser agarrado.
b) O vetor momento angular total do disco em relação ao centro do sistema pessoa-plataforma na altura dos braços, antes de ser agarrado.
c) O momento de inércia do conjunto plataforma-pessoa-disco em relação ao eixo de rotação da plataforma, após o disco ser agarrado.
d) Qual o vetor velocidade angular do conjunto plataforma-pessoa-disco após o disco ser agarrado pela mão? Girará o conjunto no sentido horário ou anti-horário?
Ver solução completaQuestão 23
Na figura abaixo observa-se uma barra fina uniforme no plano horizontal de massa desprezível e comprimento . Ela está inicialmente em repouso e presa a um eixo que passa pelo seu centro de massa e aponta na direção . Este eixo pode girar livremente. Duas partículas de massa 𝑚 e 2𝑚 se movimentam paralelamente com velocidade 𝑣 na direção () e vão se chocar simultaneamente com a barra nas suas extremidades, como mostra a figura. Após a colisão as partículas ficam grudadas na barra.
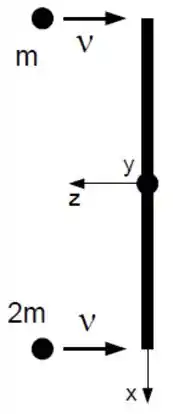
O módulo da velocidade angular do sistema logo após a colisão é igual a:
(a)
(b)
(c)
(d)
(e) 𝐴 𝑐𝑜𝑙𝑖𝑠ã𝑜 é 𝑡𝑜𝑡𝑎𝑙𝑚𝑒𝑛𝑡𝑒 𝑖𝑛𝑒𝑙á𝑠𝑡𝑖𝑐𝑎, 𝑝𝑜𝑟𝑡𝑎𝑛𝑡𝑜 𝑎 𝑣𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑𝑒 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑎𝑝ó𝑠 𝑎 𝑐𝑜𝑙𝑖𝑠ã𝑜 é 𝑧𝑒𝑟𝑜.
Ver solução completaQuestão 24
Dois astronautas, cada um tendo massa , estão ligados por uma corda de comprimento , com massa desprezível. Eles se encontram isolados no espaço, orbitando ao redor do centro de massa comum com velocidades escalares , tangenciais à corda, no sentido
mostrado na figura. Modele os astronautas como partículas.
Encontre o módulo do momento angular do sistema em relação ao centro de massa.
Os astronautas começam a puxar a corda simultaneamente de tal forma que, ao final, reduzem sua distância para . Nesta nova configuração, determine o período de rotação dos dois em relação ao centro de massa comum.
Calcule o trabalho total realizado pelos astronautas ao recolher a corda.
Ver solução completaQuestão 25
Um carrossel em forma de disco sólido homogêneo, com massa e raio , está fixo em seu centro de massa por um eixo vertical e pode girar sem atrito no plano horizontal. Partindo do repouso, o carrossel é submetido a uma aceleração angular constante de no sentido anti-horário, até atingir uma velocidade angular .
Determine o deslocamento angular realizado pelo carrossel durante seu processo de aceleração e o tempo necessário até atingir sua velocidade angular final.
Cessada a aceleração, o carrossel se mantém com velocidade angular de . Um menino de massa , correndo com uma velocidade na direção mostrada na figura, tal que , salta sobre a borda do carrossel e se agarra a ele. Modele o menino como uma partícula.
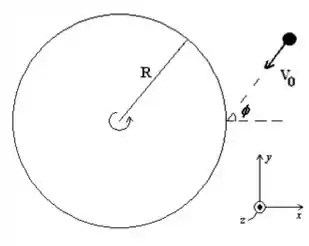
Determine os vetores angular do menino e do carrossel, respectivamente e , imediatamente antes do salto do menino sobre o carrossel(use o sistema de coordenada mostrado na figira).
Determine a velocidade angular final do conjunto carrossel menino e o sentido da rotação (horário ou anti-horário) após o menino saltar no carrossel.
Ver solução completaQuestão 26
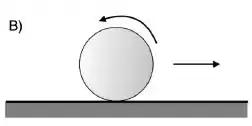
Durante uma competição de bilhar, Efren Manalang Reyes, um dos melhores jogadores de todos os tempos, atinge a bola com o seu taco como indicado na figura . O taco exerce uma força constante (alinhada com o taco como mostra a figura A) durante um intervelo de tempo , produzindo na bola um impulso linear de módulo J. A bola (massa e raio ao ser atingida pelo taco não rococheteia e move-se em linha reta para a
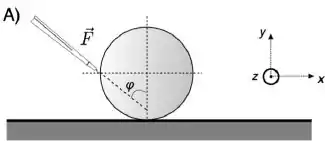
Direita, girando como indicado na figura B até um instante medido a partir do início do movimento. A partir desse instante de tempo, a bola começa a deslizar, sem girar, sobre a mesa até o instante a partir do qual começar a rolar sem deslizar. O coeficiente de atrito entre a bola e a mesa é .

Questão 27
Um carrossel de raio R e momento de inércia I em relação ao eixo de rotação está girando, sem atrito, com velocidade angular ω constante ao redor do eixo vertical, que passa perpendicularmente pelo seu centro. Uma criança de massa m, que está inicialmente em repouso no solo, salta sobre o carrossel e consegue sentar na sua borda e aí permanece. A nova velocidade angular do carrossel é:
Questão 28
ENUNCIADO A: Após um acidente, dois astronautas se encontram isolados no espaço, ligados por um cabo esticado de comprimento , e, girando com velocidade angular em relação a um eixo ortogonal ao cabo e que passa pelo centro de massa do sistema formado por eles (ver figura). Podemos considerar que as dimensões dos astronautas são muito menores que a extensão do cabo e, trata-los como se fossem duas partículas
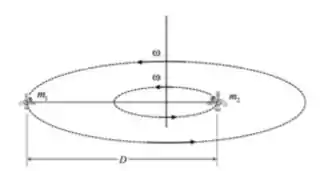
Considere o problema apresentado ENUNCIADO A. Em um dado instante, os dois astronautas começam a se aproximar puxando o cabo. Das afirmações abaixo, assinale aquelas que são corretas.
(I) O momento de inércia de cada astronauta em relação ao eixo de rotação é tal que
(II) O momento angular do sistema em relação ao eixo apresentado se manterá constante
(III) Quando a distância entre os astronautas tiver sido reduzida pela metade a velocidade angular deles será .
- Todas as afirmações são corretas
- Apenas (I) e (II)
- Apenas (I)
- Apenas (III)
- Apenas (II) e (III)
Questão 29
Em uma vareta rígida de comprimento e massa desprezível estão presas três bolinhas idênticas de massas iguais . Duas delas encontram-se unidas no centro da vareta enquanto a outra está fixa na sua extremidade. Considere que o raio das bolinhas é muito pequeno comparado com a distância . O sistema de varetas-bolinha gira com velocidade angular constante, em um plano horizontal sem atrito, em torno de um eixo que passa pelo ponto . A figura mostra o sistema visto de cima no instante . Em um certo instante de tempo posterior, uma das bolinhas do centro se solta e escorrega pela vareta pela vareta até se prender à bolinha da extremidade.
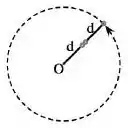
O sistema permanece girando mas passa a se mover com velocidade constante em módulo dada por:
a)
b)
c)
d)
e)
Ver solução completaQuestão 30
Duas esferas de são presas às extremidade de uma barra fina de massa desprezível, de de comprimento. A barra pode girar livremente, sem atrito, num plano vertical, em torno de um eixo horizontal que passa pelo seu centro. Enquanto a barra está na horizontal como mostra afigura, uma massinha de cai com velocidade de sobre uma das esferas e fica grudada a ela. Considerando as esferas como massa pontuais, calcule:
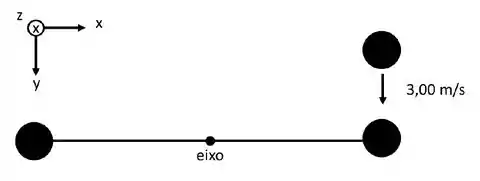
O momento de inércia do sistema em torno do eixo após a colisão.
A velocidade angular do sistema imediatamente após a colisão.
O vetor torque resultante realizado pela força peso no sistema quando a barra faz uma ângulo de com a horizontal.
Qual será o ângulo medido a partir da horizontal em que o sistema irá parar temporariamente.
Ver solução completaQuestão 31
A figura mostra uma haste homogênea vertical articulada por um parafuso , preso em sua extremidade superior e que oferece atrito desprezível. A haste tem massa e comprimento . Uma bola de neve de massa viaja em direção à haste e vai atingi-la exatamente em seu centro. No momento da colisão da bola de neve é dada pelo vetor (ver figura para o sistema de coordenadas).
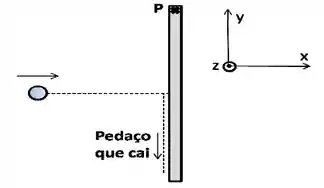
Como resultado da colisão, a bola se parte em três pedaços de igual massa . O pedaço se gruda à haste, o pedaço se solta, caindo inicialmente com velocidade , e o pedaço sai com velocidade .
Calcule, em relação ao ponto P, o vetor momento angular total do sistema antes da colisão, sabendo que a haste se encontra inicialmente em repouso. Responda ainda se haverá ou não conservação do momento angular total do sistema na colisão, justificando cuidadosamente.
Calcule, em relação ao ponto P, os vetores momentos angulares e dos pedaços e logo após a colisão.
Determine o momento de inércia do conjunto haste pedaço .
Calcule a velocidade angular da haste após a colisão e também a energia cinética de rotação do conjunto haste pedaço .
Ver solução completaQuestão 32
Uma patinadora passa a girar mais rápido ao fechar os seus braços, como ilustrado na figura abaixo.
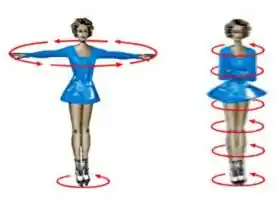
Isso ocorre porque:
(A) A patinadora sofre um torque externo que aumenta a sua aceleração angular.
(B) A energia rotacional da patinadora é conservada e, como o momento de inércia da patinadora diminui, a sua velocidade angular aumenta.
(C) O momento angular da patinadora é conservado e, como o momento de inércia da patinadora diminui, a sua velocidade angular aumenta.
(D) O centro de massa da patinadora muda e a variação de energia potencial gravitacional é convertida em rotação.
(E) Nenhuma das afirmações acima.
Ver solução completaQuestão 33
Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro
da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .
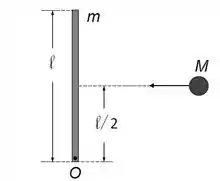
Considere as afirmativas abaixo a respeito da colisão entre a partícula e a barra:
(I) O momento linear total do sistema se conserva.
(II) A energia mecânica total do sistema se conserva.
(III) O momento angular total do sistema em relação ao ponto se conserva.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 34
(Capítulo 9.1 – Exercício 72) No sistema do problema 71, o bloco de é largado do repouso. (a) Determine a rapidez do bloco depois de ele ter caído uma distância de . (b) Qual é a rapidez angular da polia neste instante?
Ver solução completaQuestão 35
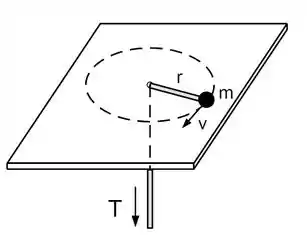
Um pequeno bloco de massa gira sobre uma superfície horizontal sem atrito e faz uma trajetória circular de raio com velocidade tangencial . O bloco está preso a uma corda de massa desprezível que passa por um furo no centro da superfície como mostra a figura. Num dado momento a corda é cuidadosamente puxada para baixo reduzindo o raio da trajetória do bloco para . Considere o bloco como uma partícula e responda:
(a) Durante o intervalo de tempo em que a corda é puxada, o momento angular do bloco em torno do furo é conservado? Justifique.
(b) Qual é a nova velocidade angular do bloco após a redução do raio da trajetória? Determine a variação de sua energia cinética.
(c) Determine a expressão literal que fornece o módulo da tensão no fio em função da massa , do raio e do momento angular em torno do furo.
(d) Seja a tensão máxima que o fio suporta igual a . Determine o raio da trajetória que o bloco percorre e a sua velocidade tangencial quando o fio estiver prestes a arrebentar.
Questão 36
Um corpo uniforme de massa está preso a um fio ideal de massa desprezível que passa por um buraco no centro da superfície. A superfície se encontra no plano . O corpo está inicialmente descrevendo uma trajetória circular em sentido anti-horário sobre a superfície horizontal com velocidade linear inicial e raio inicial medido a partir do seu centro de massa de . O fio é puxado por uma força após o fio ter passado pelo buraco conforme a figura.
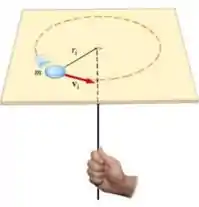
Quando a força para de atuar, o raio da trajetória final é de . Desconsidere o atrito entre o fio e o buraco e entre o corpo e a superfície.
a) Determine o vetor momento angular inicial do corpo girando em torno do eixo de rotação.
b) Determine o vetor velocidade angular final do corpo.
c) Encontre o trabalho realizado pela força sobre o corpo.
d) Marque a única alternativa correta: Após ter reduzido o raio da trajetória em relação a trajetória inicial,
(i) o momento angular e a energia cinética se conservam pois não há força externa atuando no sistema.
(ii) o momento angular se conserva pois não há forças externas produzindo um torque no sistema e a energia cinética não se conserva.
(iii) o momento angular não se conserva, pois a força produz um torque externo no sistema e a
energia cinética se conserva pois não há colisão.
(iv) o momento angular não se conserva, pois a força produz um torque externo no sistema e a
energia cinética não se conserva.
(v) o momento de inércia do sistema muda, por isso não se conservam nem o momento angular e nem a energia cinética.
(vi) Nenhuma das afirmações anteriores está correta.
Ver solução completaQuestão 37
Uma esfera maciça homogênea, de massa e raio , está fixada por sua periferia à extremidade de uma barra fina homogênea, de massa e comprimento . O conjunto barra-esfera está disposta sobre uma mesa horizontal sem atrito, de modo que pode girar livremente em torno de . Considere as seguintes expressões para os momentos de inércia em torno dos centros de massa: e .

a) Calcule, em , o momento de inércia do conjunto barra-esfera em relação ao ponto .
O conjunto barra-esfera, inicialmente em repouso, recebe o impacto de uma bala de massa que se dirige perpendicularmente à barra com velocidade escalar . Como resultado deste impacto de duração muito curta, a bala acaba se alojando exatamente no centro da esfera, e o novo conjunto, barra-esfera-bala, passa a rodar em torno de .
b) Julgue cada afirmativa como Verdadeira ou Falsa e depois justifique sua resposta.
(i) A energia cinética total do sistema barra-esfera-bala é conservada durante a colisão.
(ii) O momento linear total do sistema barra-esfera-bala é conservado durante a colisão.
(iii) O momento angular total do sistema barra-esfera-bala é conservado durante a colisão.
Considere a massa da bala e suponha que o valor encontrado no item (a) para o momento de inércia do conjunto barra-esfera tenha sido .
c) Calcule a velocidade escalar que a bala possuía imediatamente antes do impacto sabendo que, imediatamente após o impacto, o sistema barra-esfera-bala gira ao redor de com velocidade angular final .
Ver solução completaQuestão 38
Um garoto de está em pé a do centro de um carrossel que tem um momento de inércia de . O garoto e o carrossel estão ambos inicialmente parados. Num determinado momento, o garoto começa a correr em círculo, com velocidade de , em relação ao solo.
(a) Calcule a velocidade angular (módulo, direção e sentido) do carrossel.
(b) Calcule a velocidade do garoto em relação à superfície do carrossel.
Ver solução completaQuestão 39
Um bloco de inércia é preso a um bloco de inércia por uma corda que passa por um disco uniforme de inércia e raio que pode rodar em torno do seu eixo. Inicialmente, o bloco de inércia é colocado de tal forma que a corda está tensionada. Ignore o atrito entre o disco e o eixo de rotação.
- Determine a aceleração angular da polia quando o sistema é liberado.
- Se o sistema é liberado a partir do repouso, qual é a velocidade do bloco de inércia após ele ter descido uma altura ?

Questão 40
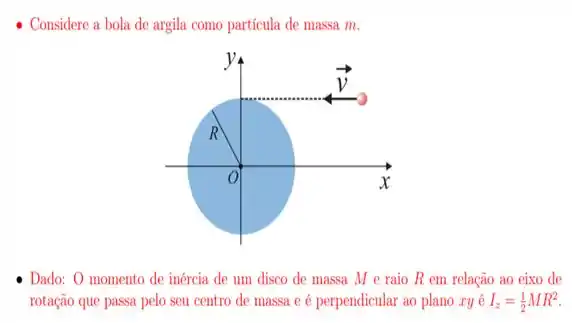
19. Uma bola de argila com massa é arremessada com velocidade ) tangencialmente à borda de um disco homogêneo de massa e raio . O disco repousa sobre uma superfície lisa (no plano ) e pode girar sem atrito em torno de um eixo fixo, que passa pelo centro do disco (o ponto da figura) e que está orientado na direção do eixo . Considerando que, ao colidir com a borda do disco, a argila gruda-se a ela, podemos afirmar que o módulo da velocidade angular do disco, em radianos por segundo, após a colisão é:
Questão 41
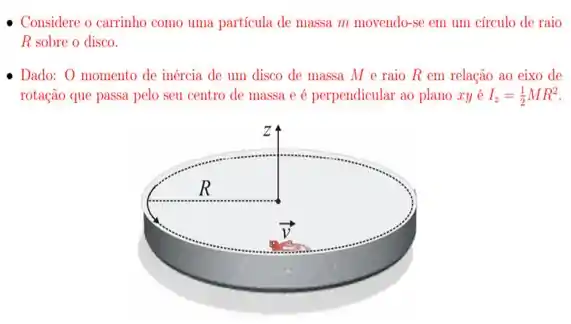
20. Um carrinho de brinquedo, de massa , move-se no sentido anti-horário na borda de um disco horizontal de forma circular, com raio e massa . Esse disco pode girar livremente, sem atrito, em torno de um eixo vertical fixo que passa pelo seu centro. Inicialmente, a velocidade escalar do carrinho (em relação ao chão) é , e o disco gira no sentido horário com velocidade angular em módulo igual a . Em dado instante, o carrinho para de se mover sobre o disco. O módulo do vetor velocidade angular do disco, em radianos por segundo, depois que o carrinho para é:
Questão 42
Uma patinadora está de pé, com os braços encolhidos, realizando uma rotação pura em torno de um eixo vertical que passa pelo seu centro de massa. Ao abrir os braços, seu momento de inércia aumenta para do valor inicial. A razão entre a energia cinética de rotação quando ela está de braços fechados, , e a energia cinética de rotação após abrir os braços, , é
a)
b)
c)
d)
e)
Ver solução completaQuestão 43
Julgue os itens abaixo em verdadeiro ou falso.
I – Torque, definido por , representa uma grandeza vetorial que pode ser aplicável a uma partícula que se mova apenas em trajetórias circulares em relação a um ponto fixo, possuindo assim orientação fixa.
II – O torque possui seu valor máximo quando a força é aplicada na direção do ponto em torno do qual o corpo é capaz de sofrer rotação
III – Visto que os torques internos de um corpo rígido ocorrem aos pares (ação e reação), um corpo que sofre ação de torques externos tem seu momento angular total (definido por ) conservado.
Todas as opções são erradas
Todas as opções são corretas
Apenas a opção I é errada
Apenas a opção II é correta
Apenas a opção III é correta
Ver solução completaQuestão 44
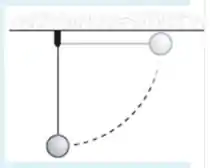
Um bloco de massa está preso a um eixo por uma corda ideal de tamanho . O bloco é solto com a corda esticada na posição horizontal.
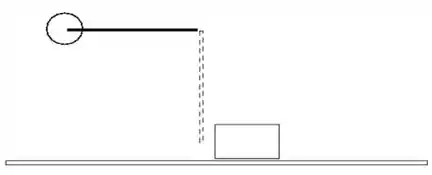
a) (0,5 pontos) Calcule a velocidade do bloco e a tração na corda no ponto mais baixo de sua trajetória;
b) (1,0 pontos) No ponto mais baixo de sua trajetória o bloco colide com um segundo bloco de massa , e recua com metade da sua velocidade. Calcule a velocidade que o bloco de massa adquire após a colisão, e a energia dissipada na colisão;
c) (1,0 pontos) Considerando que o coeficiente de atrito cinético entre o bloco de massa m e o chão é = 0,25, calcule a distância percorrida por este bloco até parar;
d) (0,5 pontos) Calcule o momento angular de cada bloco antes e depois da colisão (módulo, direção e sentido). Há conservação de momento angular? Justifique.
Ver solução completaQuestão 45
Um astronauta está ligado a uma nave no espaço através de uma corda de de comprimento, que está completamente estendida inicialmente. Sem querer, ele aciona o seu dispositivo de propulsão, adquirindo uma velocidade tangencial de módulo e passando a descrever um movimento circular uniforme. Para tentar retornar à nave, ele começa a puxar a corda lentamente de maneira que a velocidade radial pode ser desconsiderada. Considere que, por ter uma massa muito maior que a do astronauta, a nave não se move e que a massa do astronauta com seu equipamento é de .
(a) Qual a velocidade tangencial do astronauta quando está a uma distância de da nave.
(b) Qual a força que o astronauta deve fazer sobre a corda para se manter a essa distância de da nave?
(c) Ao tentar se aproximar mais da nave, a corda não suporta a tensão e se rompe. Qual será o movimento seguido pelo astronauta após o rompimento da corda? Circular uniforme, retilíneo uniforme ou retilíneo uniformemente variado?
Ver solução completaQuestão 46
Uma nave espacial isolada no espaço tem um eixo de simetria em relação ao qual seu momento de inércia é . A nave gira, inicialmente, em torno desse eixo com velocidade angular constante e com energia cinética . Aciona-se, então, um mecanismo interno da nave que reduz seu tamanho, sem perder sua simetria relativa ao eixo de rotação, de modo que ao final seu momento de inércia relativo a esse eixo se reduz a . Pode-se afirmar que a energia cinética final da nave no tamanho final é dada por:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 47
Um disco horizontal com momento de inércia em relação ao seu eixo de simetria, visto de cima, gira no sentido anti-horário com velocidade angular (valor absoluto). Um segundo disco, com momento de inércia em relação ao seu eixo de simetria, visto de cima, gira no sentido horário com velocidade angular (valor absoluto). Em um dado instante , o segundo disco é colocado em cima do primeiro, e os dois discos passam a girar juntos com uma certa velocidade angular em torno de um eixo de simetria comum. Nessa situação, a velocidade angular é:
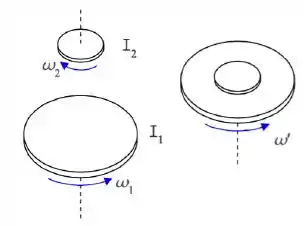
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 48
[ENUNCIADO COMUM ÀS QUESTÕES 3 E 4]
Uma pessoa possui um braço de momento de inércia e agarra uma bola de massa e velocidade inicial perpendicular ao braço. A bola é agarrada no instante a uma distância do ponto , como mostra a Figura 1. Imediatamente após receptar a bola, o sistema braço + bola gira em torno de um eixo que passa perpendicularmente ao ponto com velocidade angular . Considere que todo o movimento ocorre em um plano horizontal e que a gravidade não é relevante para a situação descrita.
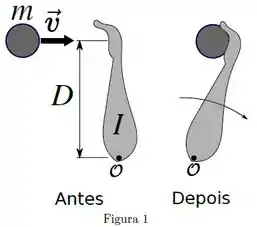
[QUESTÃO 3]
Considere as afirmativas abaixo:
- O momento angular da bola em relação ao ponto não varia em .
- A energia mecânica do sistema não varia em .
- O momento angular do sistema em relação ao ponto não varia em .
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 49
Um disco (1), de massa , raio e momento de inércia ao redor de seu centro de massa , desliza em um plano horizontal, sem atrito, com velocidade e velocidade angular (veja a figura), onde o eixo se situa para fora da folha. Em , o disco 1 colide com um disco 2 idêntico a ele, de modo que os dois saem grudados em suas extremidades.
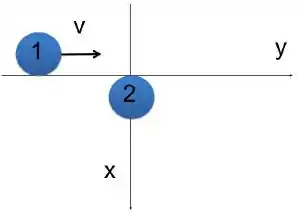
a) Dentre as grandezas seguintes: energia cinética, momento linear e momento angular, diga quais se conservam, e quais não se conservam. Justifique.
b) Calcule a velocidade do centro de massa do sistema formado pelos dois discos antes e depois da colisão.
c) Descreva o movimento do sistema formado pelos dois discos grudados após a colisão, e calcule a velocidade angular final dos discos após a colisão.
Ver solução completaQuestão 50
Um disco de massa e raio desliza ao longo de uma superfície sem atrito com velocidade . Em um dado instante de tempo , ele colide com um outro disco de massa e raio , inicialmente em repouso. A colisão acontece de tal maneira que apenas as bordas dos discos se tocam. Como as bordas dos discos estavam revestidas com uma cola de ação instantânea, os discos ficam grudados e passam a girar após a colisão. Nesse caso, determine os seguintes valores:
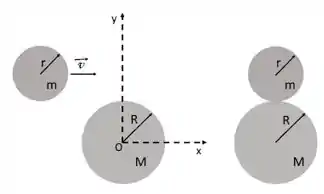
(a) A velocidade do centro de massa do sistema.
(b) A magnitude, direção e sentido do momento angular intrínseco dos discos, após a colisão, em relação ao seu centro de massa.
(c) O valor absoluto da velocidade angular dos discos após a colisão, em relação ao seu centro de massa.
Ver solução completaQuestão 51
Um disco de massa e raio está apoiado sobre uma superfície plana. Um fio inextensível, de massa desprezível, encontra-se enrolado ao redor do disco, preso a um eixo vertical. Um corpo de massa é preso a uma das extremidades do fio, que passa por uma pequena polia de massa desprezível.
Supondo que o sistema é solto a partir do repouso, e que o disco gira sem atrito, determine:
(a) A magnitude da força de tração
(b) A magnitude, direção e sentido do momento angular do disco em relação ao seu centro em um instante de tempo .
(c) Imagine agora que passado um intervalo de tempo o fio perde contato com o disco. Após o fio perder contato, um weta (o maior inseto do mundo), com massa , pousa exatamente no centro do disco. Se o inseto passa a se deslocar ao longo do raio do disco com velocidade constante , qual é o módulo da velocidade angular do disco quando o inseto se encontra a uma distância r em relação ao centro do disco?
Ver solução completaQuestão 52
Uma pessoa sentada sobre uma cadeira giratória segura uma roda de bicicleta de momento de inércia , e que gira com velocidade angular inicial . De repente a pessoa inverte o sentido da roda da bicilceta conforme a figura 2, e isso faz com que o sistema total formado pela pessoa e a roda de bicicleta gire sobre o eixo da cadeira com velocidade angular final e momento angular da pessoa. Determine e o valore de se .
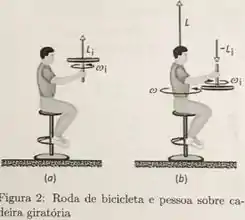
(A) e
(B) e
(C) e
(D) e
(E) e
Ver solução completaQuestão 53
Uma barra rígida, que tem sua massa distribuída de maneira uniforme em seu comprimento , está inicialmente em repouso sobre uma mesa horizontal sem atrito. Uma partícula de massa se aproxima se aproxima da barra com uma velocidade de módulo e colide com ela a uma distância de seu centro, conforme mostra a figura. Após a colisão a partícula fica alojada na barra e o conjunto composto pela barra e a partícula passa a se movimenta em conjunto.
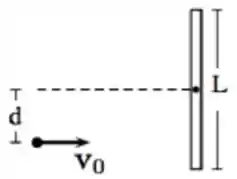
Considerando o sistema composto pela barra e a partícula, qual das quantidades a seguir não se mantém constante no processo de colisão entre a partícula e a barra?
a) Massa do sistema
b) Momento angular em relação ao ponto que, antes da colisão, coincide com o centro da barra
c) Energia cinética do sistema
d) Momento linear do sistema
e) Velocidade do centro de massa do sistema
Ver solução completaQuestão 54
No sistema ao lado, um bloco de massa está unido por um fio de comprimento a um eixo em , e uma massa está unida à por um fio de comprimento (, , ). A massa dos fios é desprezível e o conjunto está apoiado sobre uma mesa horizontal sem atrito.
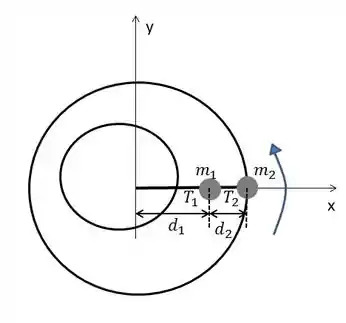
a) Sabendo que a corda que une à está sob uma tensão constante . Ache a velocidade angular constante do sistema, , e seu momento angular em relação ao ponto .
(dica: escreva a 2ª Lei de Newton para e discriminando com cuidado as tensões que agem sobre e )
b) Se o fio que liga a quebrar quando o sistema estiver passando sobre o eixo , descreva em poucas palavras o movimento subsequente de (fale sobre o tipo de movimento e a trajetória seguida e a velocidade do corpo).
c) Calcule o momento angular de após a ruptura do fio, , em relação ao ponto O.
Usando conservação de momento angular, calcule a velocidade angular final da massa ,
.
Ver solução completaQuestão 56
Um disco isolado de forças externas possui raio R e massa m e é feito de um material capaz de se reorganizar internamente. Inicialmente o material está homogeneamente espalhado por todo o disco e possui velocidade angular em torno do centro de massa. Num outro instante, toda a massa se aglomera na borda.
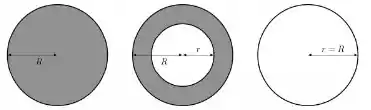
b) Encontre a velocidade angular final em função da velocidade angular inicial, justificando seu raciocínio com base em princípios físicos.
Ver solução completaQuestão 57
Um disco de raio R = 2,0 m gira sem atrito no plano horizontal, ao redor de um eixo perpendicular à sua superfície e passando no seu centro. Seu momento de inércia em relação a esse eixo vale . Uma partícula de massa m = 1,0 kg, a uma distâancia R/2 do centro do disco, gira junto com este com velocidade angular = 3,0 rad/s.
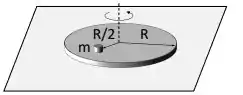
Num certo instante, a partícula escorrega e para novamente na borda do disco, a uma distância R do centro. Qual é a nova velocidade angular (em rad/s) do sistema disco + partícula?
a) 1,0
b) 1,5
c) 2,1
d) 2,2
e) 3,0
f) 3,5
g) 4,0
h) 4,4
Ver solução completaQuestão 58
Uma roda, com momento de inércia , montada em um eixo com momento de inércia desprezível, está girando com velocidade angular . Uma roda não giratória, com momento de inércia , é subitamente encaixada no mesmo eixo, como mostrado. A combinação resultante das duas rodas e do eixo girará com velocidade angular:
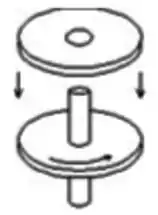
a)
b)
c)
d)
e)
Ver solução completaQuestão 59
Uma formiga de massa está parada sobre a borda de um disco de raio e massa também parado. A formiga começa a andar sobre a borda no sentido horário, com uma velocidade angular em relação ao chão. O disco gira na direção oposta da formiga, com qual velocidade angular?
- .
Dado: Momento de inércia de um disco homogêneo de massa cujo eixo de rotação passa pelo seu centro de massa:
Ver solução completaQuestão 60
Quando um homem girando em uma mesa giratória sem atrito estende seus braços (inicialmente juntos aocorpo) horizontalmente, sua velocidade angular:
- Deve aumentar.
- Deve diminuir.
- Deve permanecer a mesma.
- Pode aumentar ou diminuir, dependendo de sua velocidade angular inicial.
- Pode aumentar ou diminuir, dependendo de sua aceleração angular .
Questão 61
Uma barra homogênea de massa e comprimento pode girar em torno de um eixo fixo (ponto O) em uma de suas extremidades. Uma bola de massa de modelar, com massa e velocidade , atinge a barra a uma distância do eixo e fica grudada na barra. Dado: O momento de inércia e uma haste de massa e comprimento h em relação a um eixo que passa pelo seu centro de massa é
Momento de inércia de uma barra: .
- Que grandezas são conservadas durante a colisão? Justifique sua resposta.
- Qual o momento de inércia do sistema bola+barra em relação ao ponto O ?
- Qual o momento angular do sistema após a colisão em relação ao ponto O ?
- Qual a razão entre a energia final e a energia inicial do sistema?
Questão 62
Um besouro encontra-se na borda de um disco muito leve que gira como um carrossel. Se o besouro se deslocar para o centro do disco, assinale qual é a afirmativa verdadeira em relação ao disco e ao sistema (disco + besouro):
a) A velocidade angular do disco aumenta e o momento de inércia do sistema aumenta.
b) A velocidade angular do disco diminui e o momento de inércia do sistema aumenta.
c) A velocidade angular do disco diminui e o momento de inércia do sistema diminui.
d) A velocidade angular do disco aumenta e o momento de inércia do sistema diminui.
Ver solução completaQuestão 63
Duas bolas, cada uma de massa M, estão presas às extremidades de uma haste fina de massa desprezível comprimento . A haste está livre para girar sem atrito em um plano vertical em torno de um eixo horizontal que passa pelo centro. Com a haste inicialmente na horizontal, um pedaço de massa de vidraceiro úmida, de massa , cai sobre uma das bolas, batendo nela com uma velocidade de e ficando grudado na bola.
(a) Qual é o módulo da velocidade angular do sistema imediatamente após a batida com a massa de vidraceiro?
(b) Qual o valor mínimo de , em função de e , tal que a haste consiga dar uma volta completa?
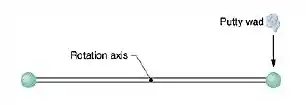
Questão 65
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a (ver figura). O fio passa sem atrito através de um orifício numa placa e é puxado lentamente para cima até que o ângulo passa a .
(a) Que comprimento do fio foi puxado?
(b) De que fator variou a velocidade de rotação?
Questão 66
Um disco de polimento, com momento de inércia , está preso a uma broca cujo motor produz um torque de módulo em relação ao eixo central do disco. O disco está inicialmente em repouso. Com o torque aplicado durante , qual é o módulo da velocidade angular do disco em relação a esse eixo, em ?
Escolha uma:
- 323,6
- 1714,97
- 1617,89
- 161,8
- 16,18
- 4,69
- 808,9
- 647,16
Questão 67
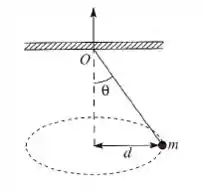
A figura mostra uma haste de massa e comprimento disposta verticalmente, e que se encontra inicialmente em repouso. A haste está pivotada na extremidade superior (ponto ) em torno da qual pode girar sem atrito. A haste é atingida a uma distância do ponto (conforme figura) por uma massa de modelar de massa que se desloca horizontalmente para a direita com velocidade escalar no momento da colisão. Após a colisão, a massa de modelar permanece grudada na haste. O momento de inércia da haste em relação ao seu centro de massa é . Considere que a massa de modelar pode ser tratada como uma partícula e .
(a) Qual é o momento de inércia do sistema (haste + massa) em relação ao eixo de rotação após a colisão?
(b) Qual é a velocidade angular ω do sistema, em função de , imediatamente após a colisão?
(c) Qual é a razão entre a energia cinética do sistema após a colisão e a energia cinética da massa de modelar imediatamente antes da colisão?
(d) Qual deve ser o valor de v para que o maior ângulo possível entre a haste e a vertical seja ?
Questão 68
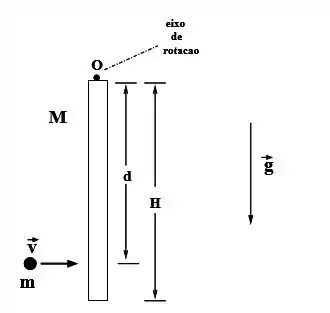
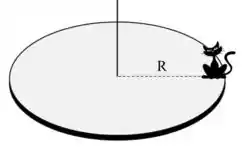
Questão 2) A figura ao lado representa um gato de massa , situado na borda de um disco de raio e massa que gira em torno de um eixo vertical que passa pelo seu centro (como um carrossel) com velocidade angular no sentido anti-horário. De repente o gato salta para fora do disco em uma dire��ão tangente à sua borda.
a) O momento angular se conserva? Justifique.
Questão 69
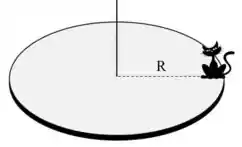
Questão 2) A figura ao lado representa um gato de massa , situado na borda de um disco de raio e massa que gira em torno de um eixo vertical que passa pelo seu centro (como um carrossel) com velocidade angular no sentido anti-horário. De repente o gato salta para fora do disco em uma direção tangente à sua borda.
b). Determine o módulo da velocidade tangencial do gato ao saltar, para que o disco inverta o sentido de rotação, passando a girar no sentido horário com metade da velocidade angular inicial (). O salto deve ocorrer no sentido horário ou anti-horário?
Questão 70
Suponha que uma pessoa está em uma cadeira giratória, girando com certa velocidade angular, com os braços abertos. Ao recolher os braços, aproximando-os do corpo,
(A) a sua velocidade angular aumenta e seu momento angular diminui.
(B) a sua velocidade angular e o seu momento angular permanecem constantes.
(C) a sua velocidade angular diminui e o seu momento angular permanece constante.
(D) a sua velocidade angular aumenta e o seu momento angular permanece constante.
(E) a sua velocidade angular e o seu momento angular aumentam.
Ver solução completaQuestão 71
Considere um disco de massa e raio girando com velocidade tangencial em torno de um eixo horizontal que passa pelo seu centro. Forneça os itens abaixo em termos de , ou .
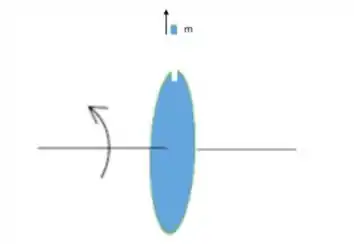
a) Calcule a energia cinética e o módulo do momento angular do disco. Mostre explicitamente o cálculo de todas as quantidades necessárias para obter estas grandezas.
b) Suponha que um pedaço do disco de massa quebra e sobe verticalmente acima do ponto do qual se desprendeu. Calcule a altura que ele sobe antes de começar a cair.
c) Qual a velocidade angular final do disco quebrado?
d) Considere o disco intacto girando em torno de um eixo paralelo ao anterior a uma distância . Calcule a razão da inércia rotacional anterior em relação a esta nova.
Ver solução completaQuestão 72
Quando a soma das forças externas e a soma dos torques externos em um corpo são ambos zero, nós podemos concluir que:
a) O corpo está rodando em torno do centro de massa com velocidade angular constante, mas não tem velocidade linear.
b) O corpo está se movendo com velocidade constante, mas não está rodando.
c) O corpo pode ter a velocidade linear ou a velocidade angular constante, mas não ambas ao mesmo tempo
d) O corpo pode ter a velocidade linear ou a velocidade angular em torno do centro de massa constante não nulas ao mesmo tempo.
e) O corpo tem velocidade linear e angular nulas.
Ver solução completaQuestão 73
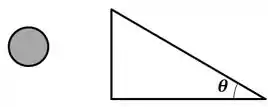
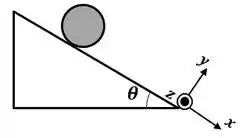
Um disco maciço de madeira de massa e raio rola para baixo sem deslizar em um plano rugoso de comprimento , inclinado de um ângulo em relação à horizontal. Utilize o sistema de coordenadas indicado.
- Desenhe as forças que agem no disco durante o rolamento. Desenho no plano, se existirem, seus pares ação-reação.
- Calcule o momento angular total do disco , em relação à origem do sistema de coordenadas, quando ele estiver no meio do plano e com velocidade do seu centro de massa ao longo do plano . Suponha que , e . Desenhe os vetores , e na figura abaixo.
- O momento angular do disco, em relação à origem do sistema de coordenadas, ao longo da descida no plano inclinado é ou não é conservado? Por que?
Questão 74
Uma patinadora está girando em torno de um eixo vertical que passa pelo seu centro de massa. Inicialmente, ela está com os seus braços abertos e gira com uma velocidade angular constante . Depois ela aproxima os braços do corpo e a velocidade angular passa a ser . Quais das alternativas que se seguem estão corretas?
(I) O momento de inércia da patinadora com os braços abertos é maior que seu momento de inércia com os braços fechados.
(II) A velocidade angular é menor que a velocidade angular
(III) O momento angular do sistema quando a patinadora está de braços abertos é igual aquele quando ela fecha os braços.
a) todas estão corretas
b) apenas (I)
c) apenas (II)
d) apenas (III)
e) apenas (I) e (II)
f) apenas (I) e (III)
g) apenas (II) e (III)
h) nenhuma está correta
Ver solução completaQuestão 75
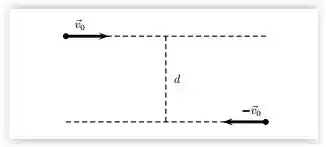
Dois patinadores de mesma massa m aproximam-se um do outro em trajetórias paralelas separadas por uma distância d, como mostrado na figura. Eles possuem velocidades de mesmo módulo . Quando passam um pelo outro, dão-se as mãos, mantendo a distância de d entre eles. Em um certo instante, os dois patinadores se puxam encurtando a distância entre eles que passa a ser , e assim permanecem. Nesta situação final, qual é a velocidade angular de rotação do sistema em torno de seu centro de massa?
- 0
Questão 76
Um aro de raio e massa gira sem atrito, no plano horizontal em torno de um eixo vertical localizado no seu centro, com velocidade angular em relação a um observador fixo no solo. Esse aro está com quatro pequenas bolas, cada uma com massa e raio desprezível, fixadas na borda, a cada radianos. Vide figura.
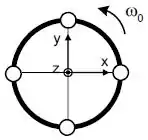
sendo: ; ; ;
a) Obtenha uma expressão literal, em termos dos dados fornecidos, para o momento angular inicial do sistema aro-quatro bolas, em relação à origem. Obtenha uma expressão literal para a energia cinética desse sistema.
Com relação aos dados do item anterior, admita que em um certo instante, duas daquelas bolas, situadas em extremidades opostas, sejam ejetadas por um mecanismo interno do aro, no mesmo sentido e direção das respectivas velocidades tangenciais dos pontos onde estão. Cada uma com velocidade de módulo igual a em relação ao mesmo observador externo.
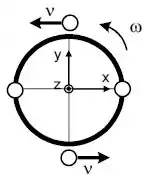
b) Encontre uma expressão literal em termos dos dados fornecidos para o módulo da nova velocidade angular do novo sistema aro-duas bolas. Explicite a lei física usada para obter os resultados.
Ver solução completaQuestão 77
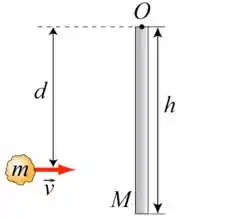
Uma barra homogênea de comprimento e massa está inicialmente em repouso. A barra pode girar sem atrito em torno de um eixo que passa em sua extremidade superior e é perpendicular ao plano da página, conforme a figura ao lado. Uma partícula de massa colide horizontalmente com a barra a uma velocidade e a uma distância do eixo de rotação. A colisão é perfeitamente inelástica e a partícula fica presa à barra após a colisão.
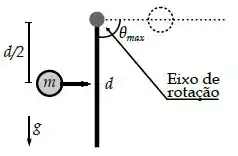
Dados: , momento de inércia de uma barra em torno de um eixo que passa pelo centro de massa .
(a) Qual é o momento de inércia do conjunto partícula+barra em relação ao eixo de rotação no instante imediatamente após a colisão?
(b) Após a colisão, a energia mecânica do sistema é conservada e verifica-se que o conjunto partícula+barra atinge um ângulo máximo . Obtenha a velocidade angular do conjunto imediatamente após a colisão.
(c) Supondo que a colisão entre a partícula e a barra ocorre durante um tempo infinitesimal, determine a velocidade do partícula imediatamente antes da colisão.
Ver solução completaQuestão 78
Um carrossel de raio e momento de inércia em relação ao centro, gira sem atrito em torno do eixo central completando uma rotação cada . Uma criança de massa que inicialmente está de pé no centro do carrossel, se desloca até a borda. Qual a velocidade angular final do carrossel em ?
Escolha uma:
Questão 79
(Cap 10 – Ex 51) Um pesado disco de plástico está montado sobre mancais sem atrito no eixo vertical que passa pelo seu centro. O disco tem raio e massa . Uma barata (massa ) está sobre o disco, a uma distância de do centro. Inicialmente, tanto o disco quanto a barata estão em repouso. A barata começa, então, a caminhar ao longo de uma trajetória circular concêntrica ao eixo do disco, à distância constante de do eixo. Se a rapidez da barata em relação ao disco é , qual é a rapidez da barata em relação à sala?
Ver solução completaQuestão 80
Um bloco de massa , preso a uma corda ideal, se move em uma trajetória circular sobre uma mesa horizontal sem atrito. A corda é puxada para baixo lentamente, através de um buraco pequeno feito no meio do círculo, diminuindo assim o raio da órbita. É correto afirmar que:
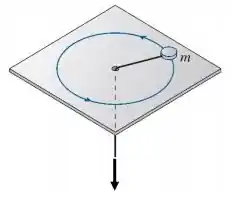
(A) A energia cinética do bloco permanece constante.
(B) A energia cinética do bloco diminui com o tempo.
(C) O momento angular do bloco diminui com o tempo.
(D) O momento angular do bloco permanece constante.
(E) Tanto o momento angular do bloco quanto a sua energia cinética aumentam com o tempo.
Ver solução completaQuestão 81
O experimento da figura consiste de uma haste horizontal delgada de comprimento 0,60 m que pode girar livremente em torno do eixo vertical que passa pelo seu C.M. O momento de inércia da haste em relação ao eixo é de 0,0060 kg.m2. Duas pequenas esferas (partículas) cada uma de massa 0,10 kg podem deslizar pela haste através de um furo existente em cada uma. Inicialmente, as esferas estão a uma distância 0,20 m e simetricamente colocadas em relação ao eixo de rotação e mantidas nestas posições mediante um fio que as une. Este sistema gira em torno do eixo com velocidade angular 12 rpm quando o fio é queimado por uma chama, as esferas deslizam até as extremidades da haste. Qual é a velocidade angular final do sistema?
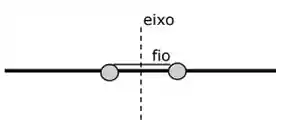
a) 1,2 rpm
b) 1,3 rpm
c) 2,2 rpm
d) 4,0 rpm
e) 5,6 rpm
Ver solução completaQuestão 82
. A soma vetorial de todos os torques que atuam sobre uma partícula é proporcional à taxa de variação temporal de qual das seguintes grandezas?
a força resultante;
momento de inércia;
a velocidade angular;
momento angular;
a energia cinética de rotação;
Ver solução completaQuestão 83
(Cap 10 – Ex 49) Você está de pé sobre uma plataforma sem atrito que está girando com uma rapidez angular de . Seus braços estão esticados para fora, e você segura um peso em cada mão. O momento de inércia do conjunto formado por você, os pesos estendidos e a plataforma é . Quando você puxa os pesos para perto do seu corpo, o momento de inércia é reduzido para . (a) Qual é a rapidez angular final da plataforma? (b) Qual é a variação na energia cinética do sistema? (c) De onde veio esse aumento de energia?
Ver solução completaQuestão 84
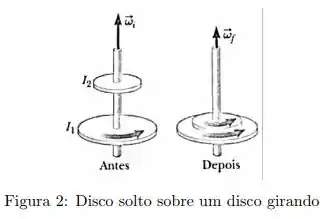
Um disco de momento de inércia gira em torno de um eixo vertical com velocidade angular . Um segundo disco, com momento de inércia e inicialmente sem girar, cai sobre o primeiro, conforme a figura 2. Por causa do atrito entre os discos, eles finalmente atingem a mesma velocidade angular . A razão vale:
A.
B.
C.
D.
E.
Ver solução completaQuestão 85
Considere o rotor de um helicóptero como sendo formado por três pás de comprimento e massa , unidas em suas extremidades (a largura e a espessura são desprezíveis em relação a). O eixo do rotor é perpendicular ao plano das pás (vide figura).
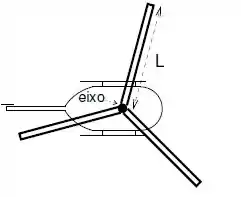
a) Calcule o momento de inércia de cada pá em relação ao eixo do rotor e o momento de inércia total do rotor.
b) Se e , calcule o torque necessário para que a velocidade angular do rotor varie uniformemente de zero a em segundos.
c) Qual a potência média transferida ao rotor nesse intervalo de tempo?
d) Considere que o momento de inércia da cabine do helicóptero em relação ao eixo do rotor seja de .Se não houvessem forças externas atuando sobre o conjunto cabine+rotor, qual seria a velocidade angular da cabine ao final do intervalo de tempo do item b?
Ver solução completaQuestão 86
Uma haste rígida de comprimento e massa está deitada sobre uma mesa sem atrito e articulada num ponto em uma de suas extremidades. Um objeto pontual de massa , vindo da esquerda e movendo com velocidade , colide com a haste elasticamente no meio dela. O objeto pontual ricocheteia e volta com uma velocidade . Depois da colisão, a haste passa a girar em torno do ponto com uma velocidade . O momento de inércia da haste para um eixo que passa pelo seu centro de massa e paralelo ao eixo articulado é . Descubra a velocidade angular em termos das variáveis apresentadas no problema.
Ver solução completaQuestão 87
Uma partícula de massa amarrada a um barbante de massa desprezível gira sobre uma mesa sem atrito, percorrendo uma circunferência de raio em torno do ponto . A pessoa que segura o barbante diminui lentamente o raio da circunferência até que .
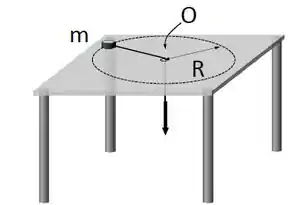
Se a velocidade angular inicial da partícula, sua velocidade angular final é:
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
Ver solução completaQuestão 88
Uma estrela em rotação sofre uma contração e seu momento de inércia diminui para do valor inicial. Qual a razão entre a energia cinética rotacional inicial, , da estrela e sua energia cinética rotacional final, ?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 89
Um sistema é constituído por duas partículas de mesma massa e uma barra fina homogênea sobre uma mesa horizontal sem atrito. As partículas estão em movimentos retilíneos uniformes com trajetórias paralelas e velocidades respectivas e . Elas colidem, simultaneamente, cada uma com uma extremidade da barra, que está em repouso e perpendicular às trajetórias, como indicado na figura. Após a colisão as partículas permanecem presas à barra e o sistema passa a girar com velocidade angular constante em torno do centro da barra.
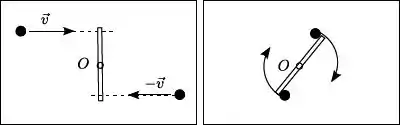
Sobre o momento linear do sistema, o seu momento angular relativo ao ponto e sua energia cinética podemos afirmar que
- Conserva-se o momento linear mas não o angular;
- Conservam-se os momentos linear e angular;
- Conserva-se o momento angular mas não o linear;
- Não se conservam os momentos linear e angular;
- Não se conservam o momento linear e a energia cinética.
Questão 90
Um disco pequeno de massa preso por um fio cuja outra extremidade está presa a um bloco de massa descreve um movimento circular uniforme de raio em uma mesa com um furo central por onde passa o fio. Sabe-se que a força de atrito entre o disco e a superfície da mesa é desprezível. Em um certo instante, uma força externa variável puxa o bloco de massa lentamente para baixo. A força externa, então, se estabiliza e observa-se que o disco passa a girar em torno do centro da mesa, em um movimento circular uniforme de raio .
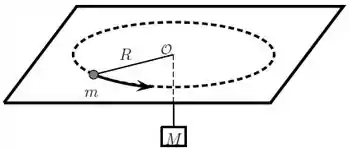
a) Qual o módulo da velocidade do disco durante o movimento circular inicial de raio ?
b) Qual passa a ser a velocidade angular de rotação quando o movimento circular passa a ter raio ?
c) Qual o trabalho realizado pela força externa que puxou o fio para que ocorra a mudança de movimento de circular de raio para o de raio ?
Ver solução completaQuestão 91
Uma partícula pontual de massa m = 1,0kg se move sobre uma superfície sem atrito com velocidade constante v = 3,0m/s. Nessa mesma superfície existe um disco homogêneo de raio R =0,50 m e massa M =10 kg que gira com velocidade angular desconhecida (inclusive seu sentido) ao redor de um eixo fixo preso a seu centro de massa. Ao alcançar o disco, a partícula se agarra a ele formando um sistema composto.
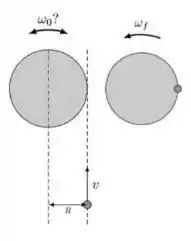
- Se a velocidade angular final do sistema, com relação ao centro de massa do disco é = 2,0rad/s no sentido anti-horário, calcule a velocidade angular Inicial do disco e indique seu sentido (horário ou anti-horário).
Questão 92
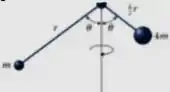
Um sistema é composto por esferas de massas: , e , conforme a Figura. O sistema gira em torno do eixo com velocidade angular , no sentido Horário pra quem vê o sistema de cima. No que segue desconsidere a Massa das hastes e considere as esferas como partículas pontuais.
- Determinar a inércia rotacional do sistema em torno do eixo
- Calcule o momento angular (módulo, direção e sentido) do sistema.
Questão 93
Considere as seguintes afirmações:
(I) A aceleração do centro de massa de um corpo rígido é igual ao quociente da força externa resultante pela sua massa total, desde que o corpo não tenha movimento de rotação.
(II) Um disco de raio gira em torno de seu eixo com uma aceleração angular . O módulo da aceleração de um ponto sobre as suas bordas vale .
(III) A energia cinética de um corpo rígido que apenas gira em torno de um eixo fixo depende somente da massa total e da velocidade angular do corpo.
(IV) Quando a força resultante sobre um corpo rígido é nula, não pode haver torque em relação ao seu centro de massa.
(V) A força resultante sobre um corpo rígido em rotação pura em torno de um eixo fixo no espaço e que passa pelo seu centro de massa é sempre nula.
(VI) Quando a velocidade do centro de massa de um sistema de partículas é nula, o seu momento angular é independente do ponto do espaço escolhido como referência.
(VII) Um corpo pode girar sem estar sujeito à ação de um torque.
Ver solução completaQuestão 94
A figura mostra uma barra homogênea vertical de comprimento e massa , em repouso, apoiada em um plano horizontal sem atrito, que pode girar em torno de um eixo em sua extremidade. Veja a figura. Uma partícula de massa e velocidade perpendicular à barra se desloca sobre o plano. Ela colide com a barra em um ponto distante do eixo, ficando grudada na barra.
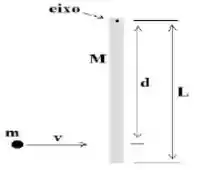
Dado: Haste:
(a) Considere a colisão. Marque com as grandezas físicas conservadas e com as não conservadas. Justifique TODAS as suas escolhas.
1-( ) Momento linear da partícula, pois...
2-( ) Momento linear do sistema barra-partícula, pois...
3-( ) Energia cinética do sistema barra-partícula, pois...
4-( ) Momento angular do sistema barra-partícula em relação ao eixo, pois...
(b) Obtenha uma expressão literal para o valor da velocidade angular do sistema barra-partícula imediatamente após o impacto em função dos dados fornecidos. Justifique claramente a lei física utilizada.
Ver solução completaQuestão 96
15) Alguns caminhões utilizam a energia armazenada em um volante que um motor elétrico acelera até uma velocidade de . Um desses volantes é um cilindro uniforme com uma massa de e um raio de . (b) Se o caminhão consome uma potência média de , por quantos minutos pode operar sem que o volante seja novamente carregado?
Ver solução completaQuestão 97
15) Alguns caminhões utilizam a energia armazenada em um volante que um motor elétrico acelera até uma velocidade de . Um desses volantes é um cilindro uniforme com uma massa de e um raio de . (a) Qual é a energia cinética máxima do volante quando está girando com a velocidade máxima?
Ver solução completaQuestão 98
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. (e) Qual é o momento de inércia da polia?
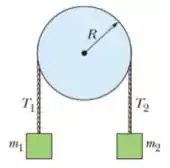
Questão 99
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. (d) Qual é o módulo da aceleração angular da polia?
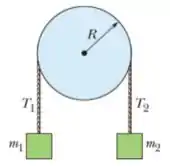
Questão 100
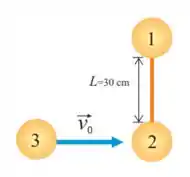
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.
(c) Determine a velocidade angular do sistema depois da colisão.
Questão 101
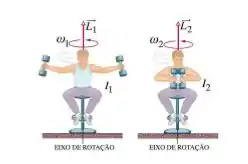
Um aluno senta numa cadeira giratória com pesos na mão. A cadeira não apresenta atrito se for girada. Inicialmente ele faz um impulso e começa a girar com velocidade angular . Nesse instante seu momento angular é e seu momento de inércia . Em seguida ele fecha os braços, conforme mostra a figura, ficando assim com momento angular , momento de inércia e velocidade angular . Após o aluno começar a girar, o torque resultante externo é nulo.
Analise as afirmativas abaixo:
Assinale a alternativa que contém apenas as VERDADEIRAS:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)
(k)
Ver solução completaQuestão 102
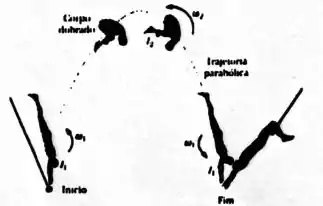
Durante um salto até o seu companheiro de número, um trapezista pretende fazer quatro cambalhotas (quatro voltas) em um intervalo de tempo . Durante o primeiro quarto da primeira cambalhota e durante o último quarto da última cambalhota, ele mantem o corpo esticado como na figura, com um momento de inércia em relação ao centro de massa. Durante o resto do percurso ele mantém o corpo dobrado, com um momento de inércia
- Qual deve ser a velocidade do trapezista em torno do eixo que passa pelo centro de massa quando ele está com o corpo dobrado?
- Qual deve ser o momento angular do trapezista em relação ao centro de massa durante o salto?
- Qual a razão entre as energias cinéticas de rotação,
Questão 103
Um carrossel de raio e momento de inércia em relação ao centro, gira sem atrito em torno do eixo central completando uma rotação cada . Uma criança de massa que inicialmente está de pé no centro do carrossel, se desloca até a borda. Qual a velocidade angular final do carrossel em ?
Escolha uma:
Questão 104
Questão discursiva.
Uma criança, com massa de , corre em direção a um carrossel, de raio igual a e momento de inércia igual a , que pode girar em torno de um eixo sem atrito.
A criança se aproxima com velocidade constante de módulo igual a tangencialmente ao carrossel, que está inicialmente em repouso.
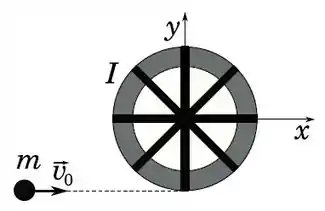
- Determine o módulo do momento angular da criança em relação ao eixo do carrossel, antes dessa pular sobre o carrossel. Considere a criança como uma partícula.
- o momento de inércia do sistema criança-carrossel;
- o módulo da velocidade angular e o sentido de rotação do sistema criança-carrossel.
A criança, então, pula e se agarra à lateral do carrossel e o sistema carrossel-criança passa a girar em conjunto com a mesma velocidade angular. Nesta situação, calcule:
Questão 105
Um aro uniforme de raio e massa está preso a um fio de massa desprezível e está girando em uma superfície horizontal. Na figura abaixo, a trajetória do centro de massa do aro está indicada pela circunferência tracejada. A trajetória tem raio e a velocidade angular do aro é . Suponha inicialmente que não há atrito entre o aro e a superfície.
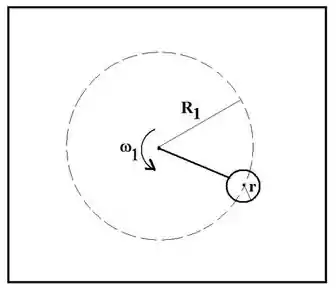
Escreva o módulo do momento angular do aro em relação ao centro da trajetória.
Um dispositivo oculto no centro da trajetória diminui o raio para . Neste novo raio, qual é o novo valor da velocidade angular ? Justifique claramente o conceito
físico utilizado.
Encontre o trabalho realizado pelo dispositivo oculto da letra b.
Suponha agora que há atrito entre o aro e a superfície. Se no instante o aro está girando na circunferência de raio (original) e com velocidade angular , e que o coeficiente de atrito estático é e o de atrito cinético é , calcule o intervalo de tempo que o aro demora em parar totalmente.
Ver solução completaQuestão 106
Uma haste de de comprimento e momento de inércia está montada horizontalmente (plano ) de modo a poder girar livremente no sentido horário em torno de um eixo na posição vertical. O eixo passa pelo centro de massa da haste.
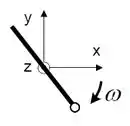
Em uma das suas extremidades está um dispositivo que lança bolinhas através de uma mola. O dispositivo tem massa desprezível e contém bolinha com momento d einércia em relação ao centro de massa da haste.
A haste é posta em rotação e alcança a velocidade angular . No instante em que o dispositivo passa pelo eixo positivo, ele lança a bolinha perpendicularmente à haste. Imediatamente após o lançamento, a velocidade angular da haste fica reduzida à metade.
- Determine a razão entre a massa da haste e a massa da bolinha.
- Determine o momento angular do sistema, em relação à origem do sistema de coordenadas, imediatamente antes do dispositivo lançar a bolinha. Determine a velocidade tangencial da bolinha imediatamente após o lançamento.
Questão 107
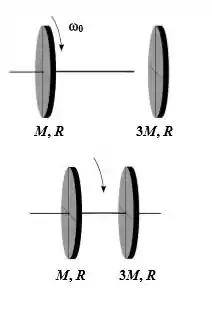
Um disco de massa e raio está girando com uma velocidade angular preso a uma haste que fura o disco através do eixo perpendicular passando pelo seu centro. Um segundo disco com massa três vezes maior que o primeiro e de mesmo raio, inicialmente em repouso, é acoplado à mesma haste de modo que o conjunto passa a girar com uma mesma velocidade angular, como mostra a figura ao lado. Dados: O momento de inércia do disco uniforme em relação ao eixo que passa pelo centro de massa é ; o momento de inércia da haste é desprezível.
(a) Determine a velocidade angular do sistema composto pelos dois discos em termos da velocidade angular .
(b) Que percentagem da energia cinética de rotação inicial é perdida devido à adição do segundo disco? Para determinar a percentagem de energia perdida utilizar a expressão onde e as energias cinéticas inicial e final respectivamente.
Questão 108
Um pequeno bloco de massa parte do repouso e desliza para baixo numa superfície curva sem atrito a partir de uma altura e depois adere a uma barra homogênea de massa e comprimento . A barra, inicialmente em repouso na vertical, então gira sem atrito em torno do eixo fixo de um ângulo antes de parar momentaneamente.
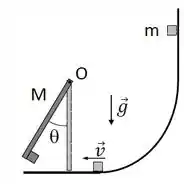
(A) Determine a velocidade do bloco após descer a superfície curva.
(B) Calcule o módulo do momento angular da massa em relação ao ponto , imediatamente antes do choque com a barra.
(C) Calcule o momento de inércia do conjunto barra + bloco em relação ao ponto .
(D) Calcule a velocidade angular do conjunto barra + bloco imediatamente depois do choque.
Dado: o momento de inércia de uma barra delgada de comprimento e massa girando sobre um eixo perpendicular à barra, passando por seu centro de massa é.
Ver solução completaQuestão 109
Uma bola de boliche de raio é lançada com velocidade sobre uma superfície plana horizontal, sem movimento rotacional. O coeficiente de atrito cinético entre a bola de boliche e a superfície é . Enquanto desliza, por causa do atrito com a superfície, a bola inicia um movimento rotacional, até que passa a descrever um movimento de rolamento, rolando sem deslizar.
- Calcule a aceleração do centro de massa e a aceleração angular da bola enquanto ela desliza sobre a superfície.
- Determine o instante de tempo no qual a bola passa a rolar sem deslizar.
Questão 110
[ENUNCIADO COMUM ÀS QUESTÕES 3 E 4]
Uma pessoa possui um braço de momento de inércia e agarra uma bola de massa e velocidade inicial perpendicular ao braço. A bola é agarrada no instante a uma distância do ponto , como mostra a Figura 1. Imediatamente após receptar a bola, o sistema braço + bola gira em torno de um eixo que passa perpendicularmente ao ponto com velocidade angular . Considere que todo o movimento ocorre em um plano horizontal e que a gravidade não é relevante para a situação descrita.
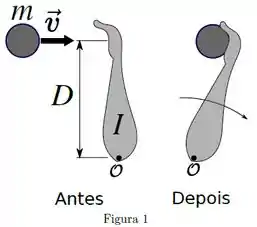
[QUESTÃO 4]
O módulo de logo antes da receptação é igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 111
Um ponto material , com massa , esta amarrado com uma corda inextensível a uma haste vertical fina, posicionada no ponto O. A haste gira e produz uma trajetória circular do ponto , com raio inicial , velocidade inicial e velocidade angular . Após algum tempo, a corda foi envolta em torno da haste e o raio da própria trajetória é reduzido para um valor final . Podemos afirmar, em relacao às magnitudes da velocidade final () e da velocidade angular final () de , que:
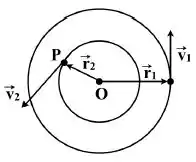
(a) e
(b) a) e c) sao corretas
(c) Nenhuma é correta
(d) ,
(e) e
Ver solução completaQuestão 112
Uma haste, muito fina e homogênea, de massa e comprimento está inicialmente parada, suspensa por um fio que passa pela metade da barra (considere o fio inextensivel e de massa despreziavel). Um projétil de massa é lançado, com velocidade perpendicular à barra contra um dos seus extremos, de forma que o projétil permanece cravado na barra e o sistema começa a girar num plano perpendicular ao eixo do fio. Nestas condições, o módulo da velocidade angular () será dado por:
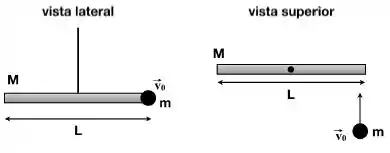
Dados: (barra)
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 113
Um disco uniforme, colocado sobre uma superfície horizontal sem atrito, possui massa e raio . O disco gira livremente ao redor de um eixo vertical passando no seu centro com velocidade angular .
Dados: Momento de inércia de um disco uniforme
- Qual o módulo do momento angular do disco em relação ao seu centro de massa?
- Num certo instante, uma partícula de massa é colocada na borda do disco e passa a girar junto com ele. Qual a velocidade angular final do sistema disco partícula?
Questão 114
Uma esfera homogênea de massa e raio está conectada sem atrito a um eixo vertical passando no seu centro. A esfera está inicialmente em repouso com um besouro de massa parado na sua linha equatorial. Num dado instante o besouro começa a se mover ao longo da linha equatorial com velocidade de módulo constante .
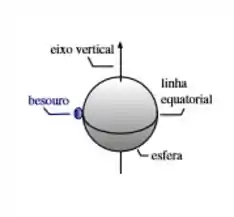
(a) Sabendo que existe atrito entre a esfera e o besouro, o momento angular total do sistema ‘esfera + besouro’ ´e conservado? Justifique.
(b) Calcule o momento de inércia do sistema ‘esfera besouro’ em relação ao eixo mencionado. Dado: Momento de inércia de uma esfera homogênea de massa e raio ao redor de um eixo passando no seu centro: .
(c) Calcule a velocidade angular que a esfera adquire quando o besouro se movimenta.
Ver solução completaQuestão 115
Uma patinadora, girando sobre si mesma em uma pista de gelo, recolhe seus braços estendidos, reduzindo assim seu momento de inércia por um fator 2. A razão entre a energia cinética final e a energia cinética inicial () é:
a) 2
b) 8
c) 4
d) 1
e) 0,5
Ver solução completaQuestão 116
Considere um sistema composto por um cilindro de massa e raio , uma haste de massa e comprimento e dois discos de massa . Os discos estão encostados no cilindro, presos por um freio, como ilustra a figura. Um torque externo coloca o sistema em rotação em torno do eixo-y no sentido horário sendo desligado quando a velocidade angular é alcançada. Neste instante o freio que prende os discos é retirado e os discos deslizam pela haste até as suas extremidades.
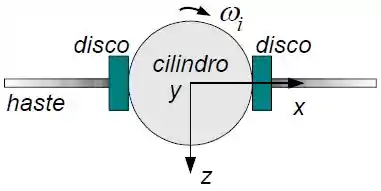
a) Encontre a nova velocidade angular do sistema quando os discos chegarem nas extremidades da haste. Considere os discos como massas pontuais.
Dados: sendo:
;
;
;
;
Ver solução completaQuestão 118
Na figura, uma partícula de massa oscila em um círculo vertical na extremidade de uma corda. A corda tem de comprimento e massa desprezível. Se a partícula é liberada com velocidade inicial zero de uma posição horizontal, o módulo de seu momento angular (em e com dois algarismos significativos) no ponto mais baixo de seu caminho em relação ao centro do círculo é de aproximadamente (utilize , se precisar para a aceleração da gravidade)