Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.Problemas adicionais - Ex. 81
Uma luz incide em uma rede de difração fazendo um ângulo com o plano da rede, como mostra a figura. Mostre que franjas claras ocorrem em ângulos que satisfazem a equação
(Compare esta equação com a Eq. 36-25.) Apenas o caso especial foi tratado neste capítulo.
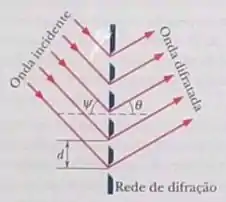
Passo 1
O que precisa acontecer para que seja formada uma franja clara? Os raio precisam sofrer interferência construtiva.
Em outras palavras, a diferença de caminho entre dois raios deve ser algum múltiplo do comprimento de onda da luz:
Então vamos procurar alguma expressão que dê a diferença de caminho entre dois raios.
Passo 2
Começamos com um diagrama simples, que represente apenas dois raios passando por fendas próximas, e algumas retas que marcam a diferença de caminho entre os dois raios:
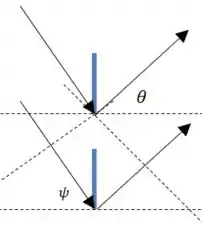
Usando um pouco de geometria, podemos identificar alguns dos ângulos nesse diagrama:
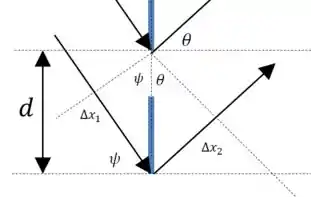
Então, pela condição que escrevemos antes:
E a equação mencionado aparece simplesmente quando fazemos . Nesse caso teríamos:
Resposta
Demonstração.